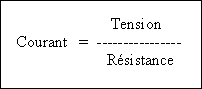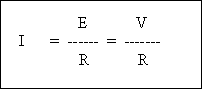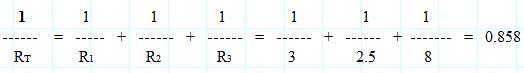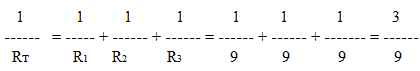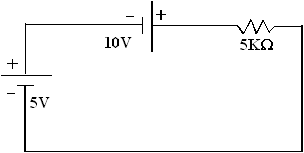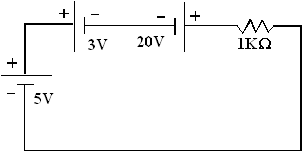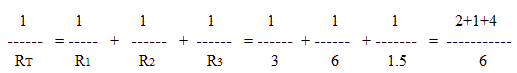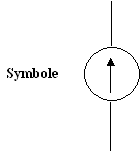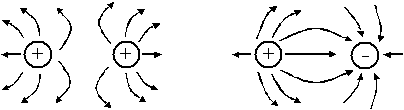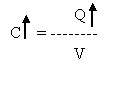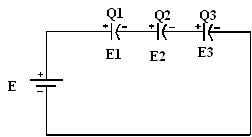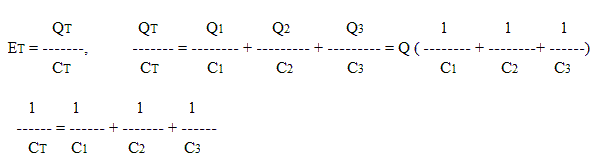Courant Continu

       1. Introduction
 2. Intensité et tension
3. Codification et classement des résistances
4. Loi d'ohm
5. Caractéristiques des résistances
6. Puissance et énergie
7. Circuit série
8. Circuit paralèle
9. Les appareils de mesure
10. Les sources de tension
11. Circuit mixte
12. Théorème de superposition
13. La résistance variable
14. Les condensateurs

1- Introduction

 L’électricité est très présente dans notre vie. À la maison, elle nous apporte l’éclairage, le chauffage, la climatisation, le téléphone, la télévision etc. Dans l’industrie, elle a rendu possibles l’informatique, la robotique etc.

 

1.      Nature de l’électricité

Les premières applications de l’électricité remontent à 1837 avec l’invention du télégraphe par Samuel F.B. Morse. Cette invention fut suivie par celle du téléphone par Graham Bell en 1876, et deux ans plus tard, par la mise au point de la lampe à incandescence par Thomas A. Edison.

De nos jours, on considère l’électricité comme un phénomène dû à la matière et non comme de la matière, de la même façon que le vent n’est pas de l’air mais un phénomène dû à l’air. Par conséquent, pour comprendre la vraie nature de l’électricité, on doit se pencher sur la structure

 

2.      États de la matière

Tout ce qui possède une masse et occupe un espace constitue de la matière. Sous l’influence de variations de température ou de pression, une substance (la matière) peut prendre l’un des trois états physiques suivants : solide, liquide, gazeux. Prenons l’exemple de l’eau : à une température se situant entre 0 et 100 ^oC, elle se présente dans un état liquide; elle possède un volume défini tout en ayant pas de forme, car elle prend la forme du contenant. À une température égale ou inférieure à 0 ^oC, c’est de la glace, donc un état solide, car l’eau possède alors une forme propre et un volume déterminé. Finalement, à une température égale ou supérieure à 100 ^oC, l’eau devient vapeur, c’est-à-dire qu’elle passe à l’état gazeux; elle n’a ni forme propre ni volume déterminé. La vapeur (gaz) a tendance à occuper le plus grand volume possible en épousant la forme de son contenant.

 Les scientifiques ont récemment découvert un nouvel état de la matière, à mi-chemin entre l’état solide et l’état liquide : la matière molle. Les cristaux liquides, qu’on utilise dans plusieurs procédés d’affichage, comme les écrans à cristaux liquides, constituent une forme de matière molle.

 La matière se compose d’un nombre limité de corps simples, qu’on appelle éléments. Les éléments ne peuvent être décomposés en substances plus simples par des moyens chimiques. On en dénombre 110 à ce jour. Lorsqu’on combine deux ou plusieurs éléments, on forme un composé. Exemple : l’eau est un composé obtenu par la combinaison de l’oxygène et de l’hydrogène. Ces deux éléments sont des gaz à l’état naturel.

2- Intensité et tension

1. L'atome et sa structure
2. Analogie eau-électricité et définitions
3. Unités et notations

 
1. L’atome et sa structure : pour bien comprendre les notions fondamentales d’intensité et de tension, il est essentiel de connaître l’atome et sa structure.

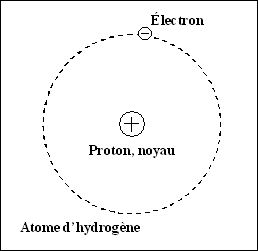
L’atome d’hydrogène se compose de deux particules, le proton et l’électron. Le proton, particule de charge positive, constitue le noyau de l’atome et l’électron décrit une orbite autour de ce dernier.

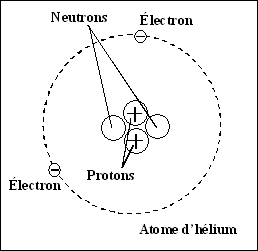
Des charges électriques de mêmes signes se repoussent alors que des chargent de signes contraires s’attirent.

Le cuivre est le métal le plus employé dans le domaine électrique (1 atome de cuivre possède 29 électrons dont un faiblement lié).

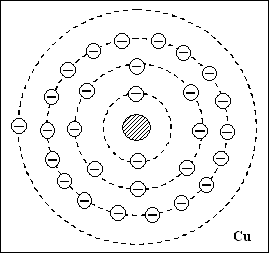
Il faut compter 2n² électrons par couche (n étant le numéro de la couche en partant du noyau). Donc pour le cuivre :

                                Première couche (n = 1) : 2 électrons

                                Deuxième couche (n = 2) : 8 électrons

                                Troisième couche (n =3) : 18 électrons

                                Quatrième couche (n = 4) : 1 électron

                                Total : 29 électrons

Il y a 4 x 10²¹ électrons libres dans 1 cm³ de cuivre. Si on arrive à déplacer ces électrons libres dans un sens déterminé, on a alors un courant électrique.

2. Analogie eau-électricité et définitions :

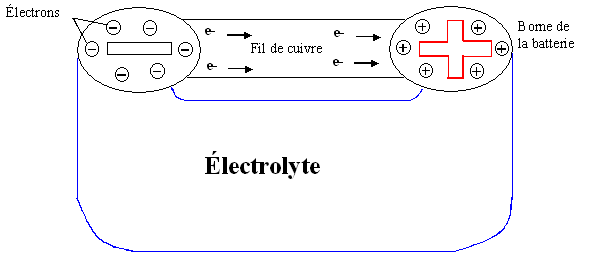
Les batteries sont des sources de tension à courant continu (déplacement unidirectionnel des électrons). Si on créait une opposition au passage des électrons, l’intensité du courant va diminuer. Cette opposition s’appelle résistance et s’exprime en ohm symbolisé Ω (oméga en alphabet grec) en l’honneur de Georg Ohm physicien Allemand 1789-1854.

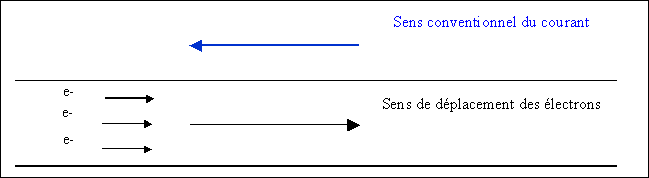
Symbole graphique et littéral de la résistance :

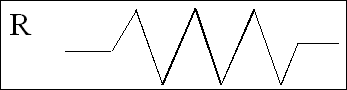
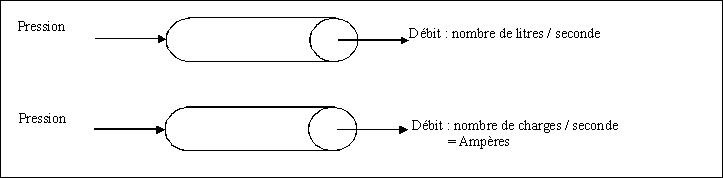
Le débit électronique est appelé intensité du courant et s’exprime en ampères (André-Marie Ampère, Physicien et Mathématicien Français 1775-1836). La pression nécessaire pour déplacer les électrons est appelée tension et s’exprime en volts. (Comte Alessandro Volta, Physicien Italien 1745-1827)

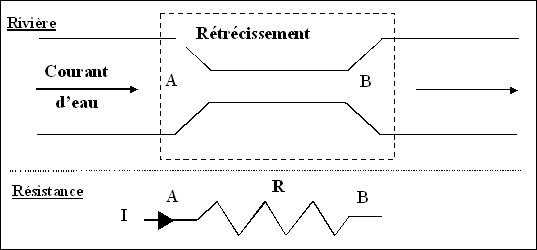
Le débit de l’eau est limité par le rétrécissement du cours d’eau, ce qui entraîne une différence de pression entre les points A et B.

Par analogie, le débit du courant électrique (débit d’électrons) est limité par la résistance. Entre les points A et B se crée une différence de potentiel analogue à la différence de pression.

Si le débit électronique est de 6.242 x 10¹⁸ électrons pendant une seconde, l’intensité du courant est alors de 1 ampère.

La charge d’un électron est de 1.6 x 10^-19 coulombs (C) (Charles Auguste Coulomb, Physicien Français 1736-1806) ; la charge portée par 6.242 x 10¹⁸ électrons est de : 6.242 x 10¹⁸ x 1.6 x 10^-19 = 1 coulomb

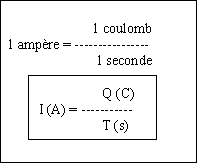
Exemple : une charge de 0.16 C passe dans un circuit en 64 ms. Déterminer le courant en ampères.

I = Q / t = 0.16 / 64 x 10^-3 = 160 / 64 = 2.5A

 

3. Unités et notations :

3.1. Les systèmes d’unités :

Les systèmes d’unités les plus communément employés par le passé étaient le système anglo-saxon et le système métrique. L’emploi de plusieurs systèmes complique inutilement les échanges techniques internationaux. Une conférence des poids et mesures a convenu d’un système international d’unités, abrégé SI dans toutes les langues en 1960. En 1973, le Canada a décidé de se convertir au système SI.

Des lettres symboliques sont utilisées en électronique aussi bien pour représenter les grandeurs que les unités. Un symbole désigne le nom de la grandeur et un autre indique l’unité de mesure de cette grandeur.

Le tableau suivant contient la liste des grandeurs les plus importantes, leur unité SI et les symboles correspondants. 

Grandeur	Symbole	Unité	Symbole
Longueur	L	Mètre	M
Masse	M	Kilogramme	Kg
Temps	t	Seconde	S
Résistance	R	Ohm	Ω
Courant	I	Ampère	A
Tension	V ou E	Volt	V
Puissance	P	Watt	W
Énergie	W	Joule	J
Conductance	G	Siemens	S
Capacité	C	Farad	F
Inductance	L	Henry	H
Fréquence	F	Hertz	Hz
Réactance	X	Ohm	Ω

 3.2. La notation scientifique :

Nous avons à travailler sur des nombres très grands et des nombres très petits. Pour faciliter la manipulation de ces nombres, nous avons recours à la notation scientifique. Cette dernière fait appel aux propriétés commodes des puissances de dix.

10⁰=1

10¹=10

10²=100

10³=1000

10^-1=1/10=0.1

10^-2=1/100=0.01

10^-3=1/1000=0.001

Pour déterminer rapidement l’exposant de 10, on compte combien il y a de chiffres entre la virgule décimale et une marque posée à droite du chiffre 1.

L’exposant est positif si le chiffre 1 est à la gauche de la virgule et négatif s’il est à sa droite.

Ainsi :

10000=1_*0000.0=10⁴

0.00001=0.00001_*=10^-5

Certaines puissances de dix étant d’emploi très fréquent, on leur a attribué des préfixes

Puissance de 10	Préfixe	Symbole
1012	Tera	T
109	Giga	G
106	Méga	M
103	Kilo	K
10-3	milli	m
10-6	micro	µ
10-9	nano	n
10-12	pico	p

Exemples :

1000000=10⁶=1M

100000=10⁵=100x10³=100K

0.0001=10^-4=0.1x10^-3=0.1m

0.000001=10^-6=1µ

3- Codification et classement des résistances

1. Les valeurs normalisées des résistances
2. Codification des résistances
3. Passage d'une puissance à l'autre
4. Propriétés des puissances de dix

1. Les valeurs normalisées des résistances :

Il serait inutile de fabriquer des résistances dans toutes les valeurs ohmiques possibles. La principale raison en est que les valeurs normalisées ont été établies de telle sorte qu’une combinaison de ces dernières suffit à créer la résistance voulue.

Dans le cas où une très grande précision serait requise, les manufacturiers d’appareils électroniques utilisent des résistances de précision fabriquées spécialement pour satisfaire leur besoin.

Les valeurs normalisées sont pour la série E24 : 

 

10        11        12        13        15        16

18        20        22        24        27        30

33        36        39        43        47        51

56        62        68        75        82        91 

    Les résistances normalisées peuvent prendre les 24 valeurs précédentes ainsi que les multiples et les sous multiples de ces valeurs.

2. La codification :

La codification des résistances nous informe de deux choses : 

   La tolérance admise (exprimée en %) quant à l’écart entre la valeur nominale annoncée et la valeur réelle de la résistance. 

Cette codification est présente sur toutes les résistances et peut revêtir deux formes : 

   La codification à l’aide du code de couleur (à 4 ou à 5 barres)

   La codification alphanumérique

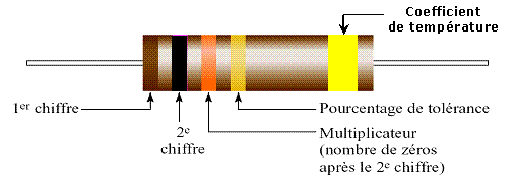
2.1 Code de couleurs des résistances à barres

        

 

Chiffres significatifs : 

2.1.1.        La première bande (premier chiffre significatif) peut prendre toutes les couleurs comprises entre le brun et le blanc (soit tous les chiffres entre 1 et 9). 

2.1.2.        La deuxième bande (deuxième chiffre significatif) peut prendre toutes les couleurs comprises entre le noir et le blanc (soit tous les chiffres entre 0 et 9). 

2.1.3.        La troisième bande indique le nombre de zéros qu'il faut ajouter aux deux premiers chiffres significatifs pour obtenir la valeur de la résistance. Deux cas particuliers :  la couleur Or indique qu'il faut diviser les deux premiers chiffres par 10 et la couleur Argent signifie qu'il faut diviser les deux premiers chiffres par 100.  

2.1.4.        La quatrième bande indique la tolérance exprimée en %

Tolérance : 

Brun         =          ± 1 %                                      Vert     =          ± 0.5 %

Rouge      =          ± 2 %                                      Bleu    =          ± 0.25 %

Or, jaune  =          ± 5 %                                      Violet  =          ± 0.1 %

Argent     =          ± 10 %                                    Gris     =          ± 0.05 %

Noir, blanc =       ± 20 %

L'absence de la quatrième bande signifie que la tolérance est de ± 20 % 

2.1.5.      La cinquième bande plus large que les autres indique le coefficient de température :  sur les résistances très précises, il peut y avoir une bague correspondant à la déviation en température. Elle s’exprime en ppm/^oC (parties par million par degré Celsius).

Exemple : soit une résistance de 1 MΩ (1 million d’ohms) qui a une déviation en température de 50 ppm/^oC. Lors de l’augmentation d’un degré de la température, la valeur de la résistance va diminuer de 50 ohms (résistance au carbone). 

Notez tout de même que cette information ne sert que très rarement. 

2.1.6.        Dans quel sens faut-il mettre la résistance pour lire sa valeur ?

 

En général, on ne peut pas se tromper, il faut mettre la bague dorée ou argentée vers la droite.

Cependant, il arrive que la résistance ait deux valeurs possibles suivant le sens dans lequel on la prend. Exemple : Brun noir rouge rouge ou rouge rouge noir brun (1000 ohms 2 % ou 24 ohms 1 %).   En fait pour faire la lecture dans le bon sens, il suffit de mettre les bagues resserrées vers la gauche.

La dernière possibilité pour savoir le bon sens de lecture est de regarder si une bague des extrémités est plus grosse que les autres. La bague la plus large doit se lire en dernier. 

Remarque : il existe des résistances à cinq bandes (6 si on compte la bande du coefficient de température). Ces résistances sont en général des résistances de précision et leur tolérance est le plus souvent de 2 % et moins : la cinquième bande est alors de couleur rouge (2%), brun (1%), vert (0.5%) etc.

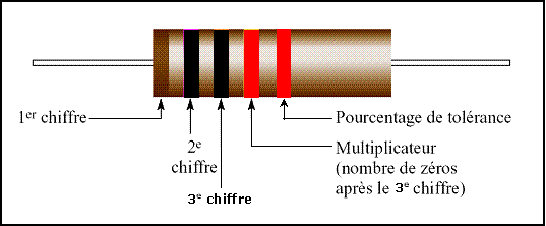
2.2 Codification alphanumérique

La codification alphanumérique des résistances consiste à inscrire, directement sur la résistance, l’information pertinente à l’aide de lettres et de chiffres. Cette technique n’est possible qu’avec des résistances dont les dimensions permettent une relecture aisée de l’information. Ce type de codification permet l’ajout d’informations absentes des résistances codées à l’aide de barres de couleur : la puissance nominale, le numéro de la pièce (pour commande au service des ventes), le nom du manufacturier (publicité).

Les résistances codées alpha numériquement utilisent les symboles associés aux préfixes affectés aux puissances de dix (K pour kilo, M pour méga). Pour simplifier l’écriture, le symbole oméga est remplacé par la lettre R, W ou E dans le cas des résistances inférieures à 1000 ohms.

Dans le même ordre d’idées, le symbole oméga est carrément omis pour les résistances supérieures à 910 ohms.

Le point décimal est remplacé par R, W, E, K ou M selon le cas.

Exemples :

1.2 Ω = 1R2 = 1W2 = 1E2

1200 Ω = 1K2

10 KΩ = 10K

15 MΩ = 15M

Tolérances : (code alphanumérique)

Lettre	B	C	D	F	G	H	J	K	M
Tolérance	0.1 %	0.25 %	0.5%	1%	2%	2.5%	5%	10%	20 %

3. Passage d'une puissance à l'autre :

On considère a et b comme étant des nombres pouvant prendre toute valeur entière. 

Soit à transformer 100 x 10^a en une puissance b : 

 

   Faire a-b ;

   Si a-b est négatif, on déplace la virgule décimale vers la gauche en ajoutant des zéros s’il y a lieu ;

   Si a-b est positif, on déplace la virgule décimale vers la droite en ajoutant des zéros s’il y a lieu.

Exemples :

- Écrire 100 x 10² en puissance de 4

                                          a = 2

                                          b = 4

                                          a-b = -2

                                          alors 100. x 10² = 1_*00.0 x 10² = 1 x 10⁴

- Exprimer 10 x 10⁵ en puissance de 3

                                          a = 5

                                          b = 3

                                          a-b = 2

                                          alors 10 x 10⁵ = 10.0 x 10⁵ = 1000. x 10³

4. Propriétés des puissances de dix (a et b pouvant être tout nombre réel positif ou négatif)

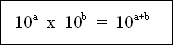
                                         10² x 10³ = 10⁵

                                         (1000)(10000)=10³x10⁴=10³⁺⁴=10⁷

                                         (0.00001)(100)=10^-5x10²=10^-5+2=10^-3

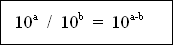
                                 100000/100=10⁵/10²=10^5-2=10³

                                         1000/0.0001=10³/10^-4=10^3-(-4)=10³⁺⁴=10⁷

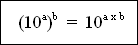
                                 (100)⁴=(10²)⁴=10^2x4=10⁸(1000)^-2=(10³)^-2=10^(3)(-2)=10^-6

                                         (0.01)^-3=(10^-2)^-3=10^(-2)(-3)=10⁶

Les exemples qui suivent montrent comment l’emploi des puissances de dix permet de simplifier des opérations portant sur des nombres arbitraires. Le principe est simple : il s’agit de faire séparément les opérations portant sur les puissances de dix de celles portant sur les chiffres significatifs.

Addition :

6300 + 75000 = (6.3)(1000) + (75)(1000) = 6.3 x 10³ + 75 x 10³ = 81.3 x 10³

Soustraction :

960 000 - 40 000 = 96 x 10⁴ - 4 x 10⁴ = 92 x 10⁴

Multiplication :

(0.0002)(0.000007) = 2 x 10^-4 x 7 x 10^-6 = 2 x 7 x 10^-4 x 10^-6 = 14 x 10^-4-6 = 14 x 10^-10

Division :

0.00047 / 0.002 = 47 x 10^-5 / 2 x 10^-3 = (47 /2)(10^-5 / 10^-3) = 23.5 x 10^-5-(-3) = 23.5 x 10-²

690 000 / 0.001³ = 69 x 10⁴ / 13 x 10^-4 = (69 / 13) x 10^4-(-4) = 5.3 x 10⁸

Élévation à une puissance :

(0.00003)3 = (3 x 10^-5)³ = 33 x (10^-5)³ = 27 x 10^(-5)(3) = 27 x 10^-15

(900 000)² = (9 x 10⁵)² = 9² x (10⁵)² = 81 x 10¹⁰

Il est possible de combiner les puissances de dix aux unités de mesure, ce qui permet d’exprimer des résultats simplement :

41200 m équivaut 41.200 x 10³ m = 41.2 Km

0.00956 g équivaut 9.56 x 10^-3 g = 9.56 mg

0.000768 s équivaut 768 x 10^-6 s = 768 µs

8400 m / 0.06 = 8.4 x 10³ / 6 x 10^-2 = (8.4 / 6) x 10^3-(-2) = 1.4 x 10⁵ m = 140 Km

4- Loi d’ohm

Toute transformation d’énergie d’une forme à une autre se fait selon la relation suivante :

  

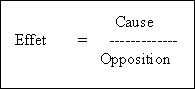
 Dans les circuits électriques, l’effet que nous tentons d’établir est le déplacement des charges, c’est à dire le courant. La tension ou différence de potentiel (d.d.p. en abrégé) entre deux points du circuit est la cause (pression) de ce déplacement de charges et l’opposition à ce déplacement est la résistance du circuit.

Appliquée aux circuits électriques, la relation devient : 

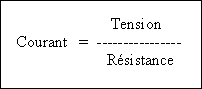
Le courant étant symbolisé par la lettre I (intensité), La tension par la lettre E ou V et la résistance par la lettre R, la relation   s’écrit : 

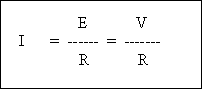
I s’exprime en ampères (A)

E ou V s’exprime en volts (V)

R s’exprime en ohms (Ω)

 

Exercice 1 : quelle est l’intensité du courant qui traverse une résistance de 2 Ω si la chute de potentiel à ses bornes est de 16 volts ?

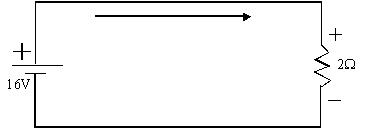
                                                              V              16

                                                I   =    --------   =   -------   =   8 A

                                                              R               2

À noter : la polarité de la chute de tension aux bornes de la résistance est déterminée par le sens du courant comme indiqué sur la figure précédente.

Exercice 2 : calculer la tension qui doit être appliquée à la résistance R pour qu’un courant de 1.5 A y circule ?

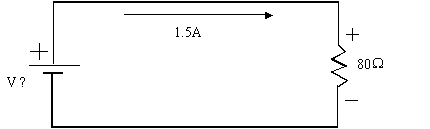
                                                V   =   R x I   =   80 x 1.5   =   120 V

Exercice 3 : calculer la valeur de la résistance R si elle est traversée par un courant de 0.4 A et que la d.d.p. à ses bornes est de 120 V ?

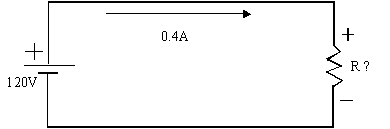
                                                               V              120

                                                R   =    --------   =   -------   =   300 Ω

                                                               I                0.4

L’intensité du courant passant dans un circuit n’est limitée que par la valeur de la résistance R. Plus la résistance est élevée, plus petite est l’intensité du courant et vice versa comme l’établit la loi d’ohm.

 

5- Caractéristiques des résistances

1. Généralités
2. Effets thermiques
3. Puissance nominale des résistances
4. Section nominale des conducteurs

1.Généralités :

La résistance d’un fil dépend de trois facteurs :

   La longueur du fil en mètres

   L’aire ou (section) du fil en mètres carrés

   La résistivité du matériau utilisé

                                                                                    l

                                                    R =   ρ     x     -------------

                                                                                   A

La résistivité ρ est une constante caractéristique du matériau conducteur. Par définition, c’est la résistance d’un fil de 1 m de longueur et de 1 m² de section, mesurée à 20 ^oC. Son unité est l’ohm-mètre (Ω.m).

Résistivité de certains matériaux :

Matériau	ρ en Ω.m à 20oC
Argent	16.4x10-9
Cuivre	17.2x10-9
Or	24.4x10-9
Aluminium	28.2x10-9
Fer	123x10-9
Carbone	34860x10-9

Exemple : Quelle est la résistance d’un fil de cuivre d’une longueur de 130 m et d’une section de 1.5 mm² ?

                                        --------------------------------

Cuivre              =>    ρ = 17.2x10^-9 Ω.m

Longueur          =>    l = 130 m

Section            =>    A = 1.5 mm² = 1.5x10^-6 m²

 

                l                                      130

R =  ρ  ------- = 17.2 x 10^-9 x ---------------- = 1.49 Ω

              A                                   1.5 x 10^-6

2. Effets thermiques :

La résistance de la plupart des matériaux conducteurs augmente avec la température, en raison de l’agitation accrue des molécules du matériau qui gêne le passage des charges. La résistance du cuivre et de la plupart des autres matériaux conducteurs augmente de façon presque linéaire avec la température.

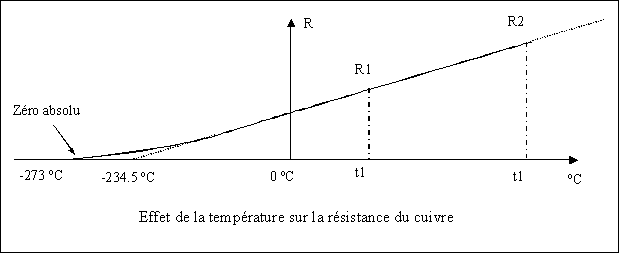
R2 = R1 [ 1 + α ( t2 - t1) ]

α étant le coefficient de température propre à chaque matériau

Coefficient de température de certains matériaux à 20 ^oC

    Argent     =     0.0038

    Cuivre     =     0.00393

    Aluminium     =     0.00391

    Carbone     =     -0.0005

Remarque : parmi les conducteurs, seul le carbone possède un coefficient de température négatif c’est à dire que sa résistance diminue lorsque la température augmente.

3. Puissance nominale des résistances :

En plus de la valeur requise en ohms, une résistance doit avoir une puissance nominale assez grande pour supporter le courant qui la traverse sans trop chauffer.

Résistance au carbone (T^o maximale  = 85 ^oC)

Résistances bobinées (T^o maximale   = 300 ^oC)

Si une résistance chauffe trop, sa valeur ohmique peut se modifier sensiblement, elle peut aussi se détruire.

La puissance nominale des résistances dépend de leurs dimensions :

 Plus la dimension est grande, plus élevée est la puissance nominale ;

 Les résistances de puissance élevée peuvent fonctionner à des températures plus élevées ;

 Les résistances bobinées ont des puissances nominales plus élevées que les résistances au carbone.

4. Section nominale des conducteurs :

Les fils ont des diamètres différents et sont identifiés d’après un numéro de calibre normalisé, appelé calibre AWG (American Wire Gage) d’utilisation courante en Amérique du Nord.

Plus le numéro de calibre  est élevé, plus la grosseur du fil est petite. La grosseur d’un fil est exprimé par un unité de surface d’un cercle, le mil circulaire, dont l’abréviation est CM (Circular Mil). Un mil circulaire est la surface d’une section de fil dont le diamètre est de 0.001 pouce = 0.0254 mm = 1 mil. Vous pouvez trouver la surface du cercle en exprimant le diamètre en mils et en élevant au carré :

A = d²  où A est l’aire en CM et d le diamètre en mils

Note : Pour des conducteurs de câbles de construction résidentielle; mode pose : pas plus de trois conducteurs sur chemins de câbles, sous une même gaine ou enfouis.

Remarque : 1 mm² = 1973.53 CM

 

La section des conducteurs est normalisée. Chaque section possède un courant admissible maximal.

 

Ce tableau n’est pas exhaustif. Plus le conducteur est gros, plus il pourra supporter des courants élevés.

6- Puissance et énergie

1. La puissance : La puissance est la quantité de travail qui peut être fournie en un temps déterminé c’est-à-dire le quotient du travail accompli par unité de temps (1 seconde) :

                                                   W (J)

                                          P = --------

                                                    t (s)

P s’exprime en J/s qui reçu le nom de watt en l’honneur de James Watt (mécanicien et ingénieur Écossais 1736-1819).

En électricité, lorsque les extrémités d’un conducteur sont reliées aux bornes d’une batterie, les électrons ont alors suffisamment d’énergie pour atteindre la borne positive vers laquelle ils sont attirés. La différence de potentiel ou tension entre les bornes de la batterie est appelée force électromotrice (f.é.m.).

Par définition, la f.é.m. est de 1 volt, si l’énergie nécessaire à déplacer une charge de 1 coulomb est de 1 joule.

                 W

 V   =   ------------   =>   W   =   Q x V

                 Q

 

 

                 Q                Nombre de charges

or I   =   --------   =   -------------------------

                 t                        Seconde

 

=>         Q     =     I x t

 

donc      W     =     I x t x V

 

             W                 I x t x V

P   =   ---------   =   -------------   =   I x V

              t                      t

 

                    P s’exprime en watt (W)

                    V s’exprime en volt (V)

                    I s’exprime en ampère (A)

 

P peut s’écrire aussi :     P     =     R x I x I     =     R x I²

 

                                          V              V²

                    P   =   V   x   ------   =   -------

                                          R              R

 

2. Énergie :                 W   =   P x t

Énergie (kilowatts x heures) = puissance (Kilowatts) x temps (heures)

(1KWh vaut 6.08 cents en décembre 2020  pour les 30 premiers KWh par jour et 9.38 cents le KWh pour le reste; 1 wattheure = 3600 joules)

Exercice 1 : calculer la puissance fournie au moteur.

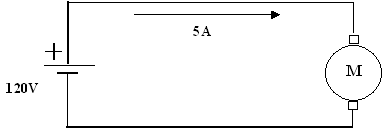
P = V x I = 120 x 5 = 600 W

Exercice 2 : quelle est la puissance dissipée dans une résistance de 5 W traversée par un courant de 4 A ?

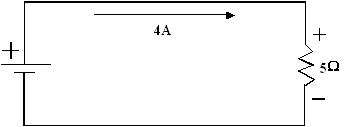
P = R x I² = (4)² x 5 = 80 W

Exercice 3 : combien en coûte t-il pour faire fonctionner un climatiseur de 2080 W 12 heures par jour pendant 60 jours, si le prix du kilowattheure est de 6.08 cents ?

-----------------------------------

W = P x t = 2.08 KW x 12 h x 60 = 1497.6 KWh

Coût = 1497.6 x 6.08 = 9105.41 cents = 91.05 $ 

Exercice 4 : combien de temps faut-il à un récepteur de télévision de 205 watts pour consommer 4 KWh d’électricité ?

-----------------------------------

P = W / t   =>   t = W / P = 4000 / 205 = 19.51 heures

Exercice 5: combien en coûte t-il au total pour alimenter :

a. Un grille pain de 1200 W pendant 30 minutes ;

b. Six ampoules de 60 W pendant 4 heures ;

c. Une machine à laver de 400 W pendant 45 minutes ;

d. Une sécheuse électrique de 5600 W pendant 20 minutes ?

Un kilowattheure coûte 6,08 cents.

-----------------------------------

W = 1.2 x 0.5 + 6 x 0.060 x 4 + 0.4 x 0.75 + 5.6 x 0.33 = 4.188 KWh

Coût : 4.188 x 6,08 = 25.46 cents

Exercice 6 : la puissance nominale d’une résistance de 1000 Ω est de 0.5 W. Quelle est l’intensité maximale du courant qui peut traverser la résistance sans l’endommager ?

-----------------------------------

P = V x I = R x I²   =>

Exercice 7 : la puissance fournie à une résistance de 7.2 KΩ est de 88 W. Quelle est la chute de tension aux bornes de la résistance ?

-----------------------------------

P = V x I = = V² / R =>  

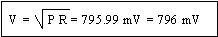
Exercice 8 :

a) Le circuit électrique d’une maison a une capacité de 60 A sous 120 volts ; calculez la puissance maximale que peut recevoir le circuit ?

b) Le propriétaire de la maison peut-il sans danger faire fonctionner en même temps les appareils suivants :

. Une sécheuse de 3000 W

. Une cuisinière de 2400 W

. Un fer à vapeur de 1000 W

. Un climatiseur de 2080 W

-----------------------------------

a) P = V x I = 120 x 60 = 7200 W

b) PT = 3000 + 2400 + 1000 + 2080 = 8480 > 7200 (puissance admise)

3. Transfert maximum de puissance d’un circuit à un autre :

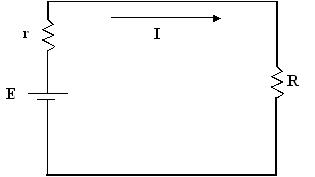
Courant I dans le circuit : 

I = E / (r + R) 

Puissance dans la charge : 

P= R x I² = R x E² / (r + R)² 

       Exemple pratique : E = 100 volts, r = 8 Ω

 

R (Ω)	P (W)	I (A)
0	0	12.5
2	200	10
4	278	8.3
6	306	7.1
8	312.5	6.25
10	308.6	5.6
12	300	5
14	289	4.5
16	278	4.2

P est la puissance absorbée par la charge. La puissance est maximale lorsque r = R. Lorsque R est petit devant r, la puissance est plus faible et le courant plus élevé, il y a alors risque de détruire les transistors (ou IC -Circuit Intégré-) de sortie de l’amplificateur.

7- Circuit série

En électricité et en électronique, un circuit est un ensemble d’éléments reliés entre eux par des conducteurs, offrant au moins un trajet fermé dans lequel peuvent circuler des charges électriques. Une branche d’un circuit est une partie de cet ensemble ; elle est constituée d’un ou de plusieurs éléments montés en série.

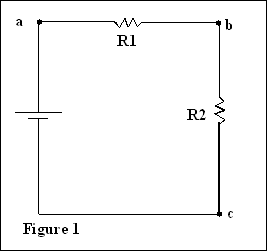
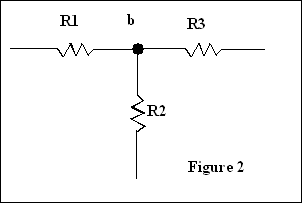
Deux éléments sont en série si la borne de l’un est reliée à la borne de l’autre sans être raccordée à la borne d’un troisième élément. Ainsi les résistances R1 et R2 de la figure 1 sont montées en série puisqu’elles ne possèdent que le point (b) en commun auquel n’est raccordée aucune autre branche. Ce n’est toutefois pas le cas des résistances R1 et R2 de la figure 2 puisque le point (b) est également le point de raccordement de la résistance R3.

Pour calculer la résistance totale d’un circuit série, il suffit de faire la somme des valeurs ohmiques de chacune des résistances du circuit. À titre d’exemple, la résistance totale du circuit de la figure 1 est égale à R1 + R2.

En règle générale, la résistance totale d’un montage en série de (N) résistances est égale à la somme des valeurs ohmiques des (N) résistances :

RT = R1 + R2 + R3 + ......... + RN

Exercice 1 : calculer la résistance totale du circuit série suivant :

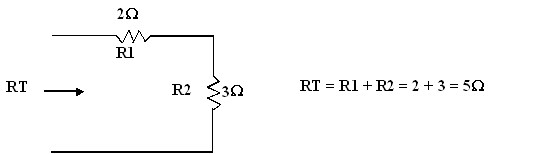
Exercice 2 : calculer la résistance totale du circuit série suivant :

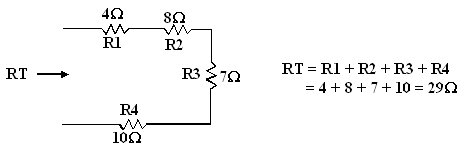
Exercice 3 : calculer la résistance totale du circuit série suivant :

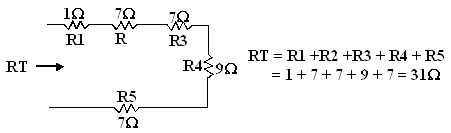
Dans un circuit série, l’intensité du courant est la même dans chacun des éléments. Par conséquent l’intensité du courant qui traverse chacune des résistances du circuit est égale à celle débitée par la batterie.

Exercice 4 : calculer l’intensité du courant I pour les trois circuits précédents si la tension V est de 12 volts.

-----------------------------------

. Exercice 1 : I = V / R = 12 / 5 = 2.4 A

. Exercice 2 : I = V / R = 12 / 29 = 414 mA

. Exercice 3 : I = V / R = 12 / 31 = 387 mA

 

Exercice 5 :

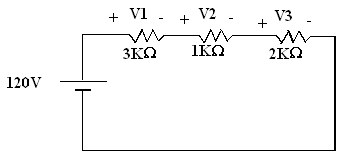
- Déterminez la résistance totale, le courant total et les chutes de tensions V1, V2 et V3

- Calculez la puissance dissipée par chacune des résistances et comparez la puissance fournie à la puissance dissipée.

----------------------------------------------------

RT = R1 + R2 + R3 = 3 K + 1 K + 2 K = 6 KΩ

IT = V / RT = 120 / 6000 = 20 mA

V1 = R1 x I1 = 3000 x 0.02 = 60 V

V2 = R2 x I2 = 1000 x 0.02 = 20 V

V3 = R3 x I3 = 2000 x 0.02 = 40 V

P1 = V1 x I1 = 60 x 0.02 = 1.2 W

P2 = V2 x I2 = 20 x 0.02 = 0.4 W

P3 = V3 x I3 = 40 x 0.02 = 0.8 W

PT = P1 + P2 + P3 = 1.2 + 0.4 + 0.8 = 2.4 W = Puissance dissipée

Puissance fournie par la batterie : P = V x I = 120 x 0.02 = 2.4 W

=> Puissance fournie = Puissance dissipée.

 

8- Circuit parallèle

Deux éléments ou deux branches sont en parallèle s’ils ont deux points en commun.

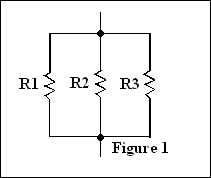
À la figure 1, les résistances R1 et R2 sont en parallèle entre elles, et en parallèle avec la résistance R3. Chacune des résistances étant en parallèle avec les autres résistances, le montage est appelé circuit parallèle.

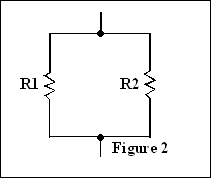
Les résistances R1 et R2 de la figure #2 sont en parallèle puisqu’elles sont raccordées à deux points communs a et b.

La tension aux bornes d’éléments en parallèle est la même pour chaque élément.

L’inverse d’une résistance s’appelle conductance et est noté G.

               1

G   =   -------

              R

Dans un circuit parallèle     GT     =     G1     +     G2   (Figure #2)

 

                1                                             1             1

GT   =   --------   =   G1     +     G2   =   ------  +  ------

               RT                                           R1            R2

 

En général     GT    =      G1     +     G2     +     G3     +     ...     +     GN

 

   1              1             1             1                      1

------   =   -------  +  ------  +  ------  +  .....  +  -------

  RT            R1           R2           R3                   RN

 

Exercice 1 : Calculer la résistance totale du circuit suivant :

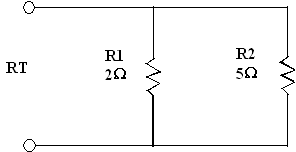
GT   =   G1     +     G2

               1                1

G1   =   -------   =   ------   =  0.5 Ω^-1

              R1                     2

 

 

               1               1

G2   =   -------   =   ------   =   0.2 Ω^-1

              R2                    5

 

GT   =   0.5     +     0.2   =    0.7 Ω^-1

 

              1               1

RT   =   ------   =   ------   =   1.429 Ω

             GT                 0.7

Exercice 2 : Calculer RT du circuit suivant :

 

 

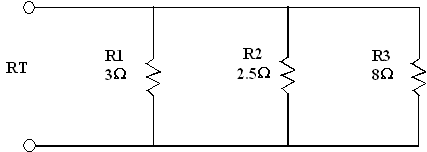
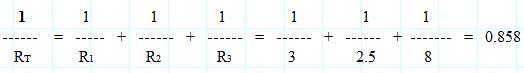
               1

RT  =  -------  =  1.165 Ω

            0.858

Exercice 3 : Calculer RT du circuit suivant :

 

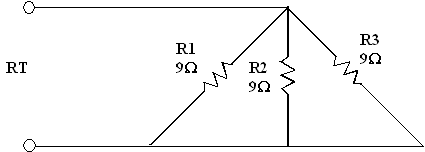
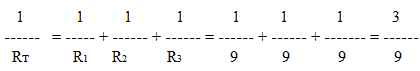
              9

RT = ------- = 3 Ω            

             3

9- Les appareils de mesure

1. Principaux renseignements indiqués sur l’appareil :

   La forme du courant (ou de la tension) pour laquelle il est prévu

_ Continu seulement

~ Alternatif seulement 

   La tension continue maximale d’utilisation

   La tension alternative maximale d’utilisation

   Le courant maximum d’utilisation

   Les différentes fonctions de l’appareil

2. Qualités de l'appareil :

          Fidélité : un appareil est fidèle s’il donne toujours la même valeur lorsqu’on lui fait mesurer la même grandeur (lectures répétitives). 

         Justesse : un appareil est juste s’il donne la valeur exacte de la grandeur mesurée. 

         Sensibilité : un appareil est d’autant plus sensible qu’il peut déceler une petite variation de la grandeur mesurée. 

         Calibre : le calibre indique la plus forte valeur mesurable par l’appareil (exemple : sur le calibre 400 volts, la valeur maximale que l’on peut mesurer est de 400 volts) 

         Résolution : c’est l’écart entre deux valeurs voisines 

         Précision : c’est le pourcentage d’erreur sur la mesure 

3. Mesure de courant :

L’appareil servant à mesurer le courant électrique s’appelle ampèremètre. Lorsqu’on mesure un courant électrique, on mesure la quantité d’électrons circulant dans le circuit. Pour ce faire, l’appareil doit toujours être branché en série avec le composant dont on désire mesurer l’intensité du courant.

Les précautions à prendre pour s’assurer de la validité des mesures sont :

-        Pour mesurer un courant continu dans un circuit, on doit sélectionner la fonction “DC”

-        Choisir l’échelle adéquate pour avoir une meilleure précision

-        Brancher l’ampèremètre en série pour éviter de l’endommager. Pour ce faire, on doit débrancher le circuit pour l’y insérer.

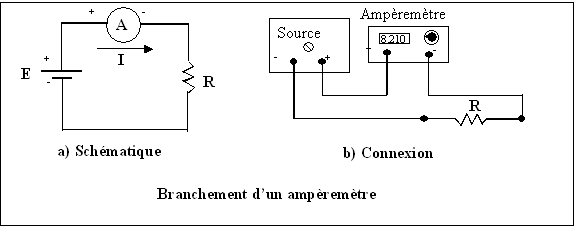
Lors du branchement, on doit s’assurer que le courant entre dans la borne positive et sort par la borne négative de l’appareil (voir figure ci-dessus).

L’ampèremètre étant branché en série, il est très important qu’il ait la plus basse valeur possible de résistance interne afin de réduire au minimum son influence dans le circuit.

Exemple

 

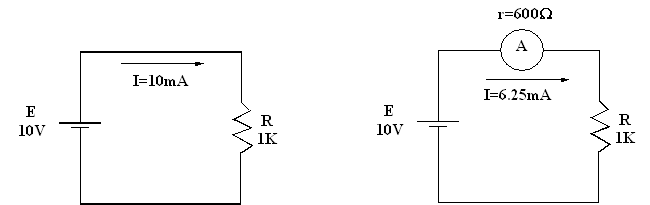
Écart = 10 mA – 6.25 mA = 3.75 mA  =>  Pourcentage d’erreur = 3.75 x 100 / 10 = 37.5 % 

Si on refait le même travail avec une résistance interne de 5 Ω, le pourcentage d’erreur est alors de : I = 10 / (1000 + 5) =9.95 mA  =>  Pourcentage d’erreur =0.05 x 100 / 10 = 0.5 % 

4. Le voltmètre :

C’est un instrument de mesure servant à évaluer quantitativement la chute de potentiel (tension) aux bornes d’un ou de plusieurs éléments dans un circuit électronique.

Le voltmètre doit toujours être branché en parallèle avec le composant dont on veut évaluer la chute de tension (surveiller les polarités)

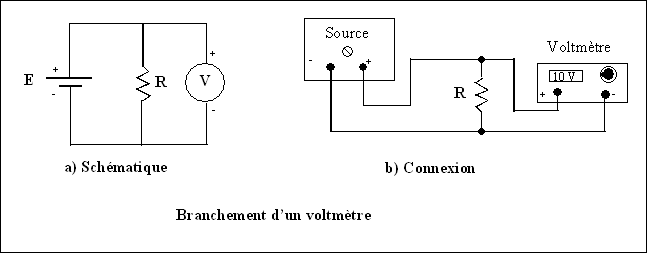
Le voltmètre étant branché en parallèle, il est très important qu’il ait la plus haute valeur possible de résistance interne afin de réduire au minimum son influence dans le circuit.

        Exemple

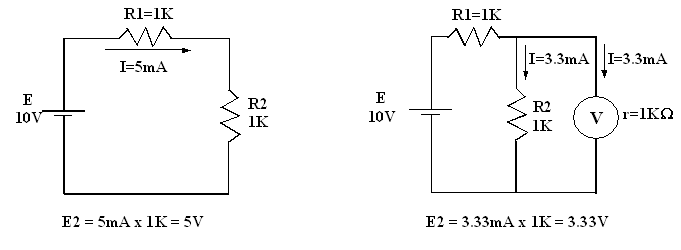
Écart = 5 – 3.33 = 1.67 V  =>  Pourcentage d’erreur = 1.67 x 100 / 5 = 33.4 %

Si on refait le même travail avec une résistance interne de 100 KΩ

I = 10/1990.1 = 5.025 mA, E2 = 4.975V

Écart = 5 – 4.975 = 0.025 V  =>  Pourcentage d’erreur = 0.025 x 100 / 5 = 0.5 %

 

10- Les sources de tension et de courant

1. Sources de tension en série:

plusieurs sources de tension en série peuvent être remplacées par une seule source de tension dont la f.é.m. est de grandeur et de polarité égales à celles de la f.é.m. résultante. On détermine la résultante en prenant la somme de toutes les f.é.m. de même polarité, et en soustrayant la somme de toutes les f.é.m. de polarité opposée.

Exercice 1 :

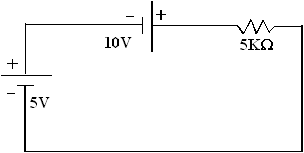
V = V1 + V2 = 5 +10 = 15 volts 

Exercice 2 :

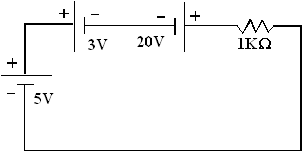
V = (20 + 5) - (3) = 22 volts 

Exercice 3 : simplifiez les circuits suivants en réduisant le plus possible le nombre de sources de tension.

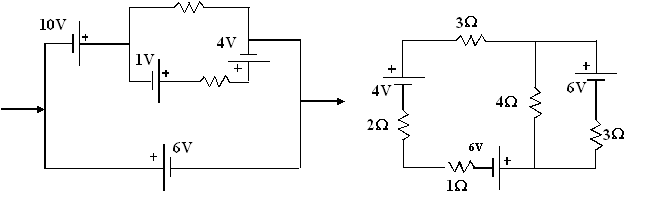
2. Résistance interne des sources de tension :

Toute source de f.é.m., qu’il s’agisse d’une génératrice, d’une batterie ou d’une alimentation de laboratoire a une certaine résistance interne. Le circuit équivalent réel d’une source de f.é.m. est donc semblable à celui-ci :

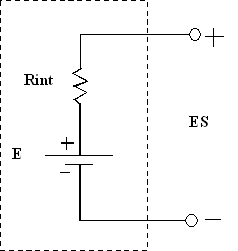
Exercice 1 : calculez la résistance interne d’une batterie qui, en l’absence de toute charge, fournit une tension de sortie de 60 volts et qui en présence d’une charge de 28 W, débite un courant de 2A.

 

-----------------------------------

 VR = R x I = 28 x 2 = 56 volts      =>    VRint = 60 - VR = 60 - 56 = 4 volts

                                                     =>    Rint = 4 / 2 = 2 Ω

Exercice 2 : calculez la tension ES et la perte de puissance dans la résistance interne de la boîte noire suivante :

 

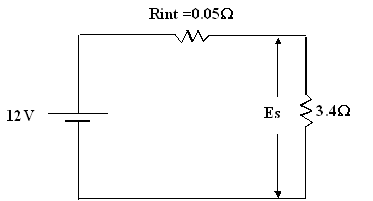
I = V / RT = 12 / 3.45 = 3.48 A

Es = 3.4 x 3.48 = 11.83 volts

P = R I² = 0.05 x (3.48)² = 0.6 watt

 

 

  
3. Loi des tensions de Kirchhoff :

la loi des tensions de Kirchhoff s’énonce : la somme algébrique des différences de potentiel le long d’un circuit fermé (boucle) est nulle.

 

 

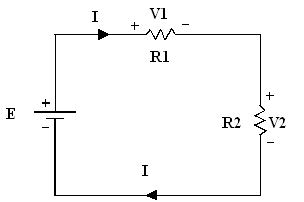
+E - V1 - V2 = 0   =>    E = V1 + V2 

La somme des f.é.m. = La somme des chutes de tension

 

 

Exercice 1 : déterminez V1 et V2 dans les circuits suivants :

 

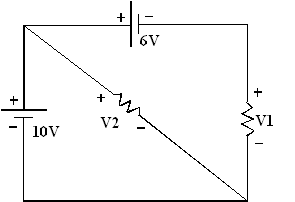
 10 - V2 = 0 => V2 = 10 volts

 V2 - 6 - V1 = 0 => V1 = V2 - 6

V1 = 10 - 6 = 4 volts

 

 

 

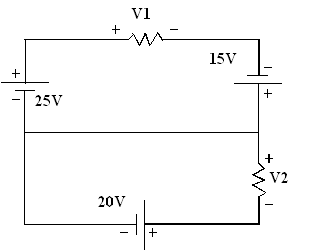
25 - V1 + 15 = 0  => V1 = 40 volts

20 + V2 = 0 => V2 = - 20 volts 

 

 

Exercice 2 : Pour le circuit suivant,

 

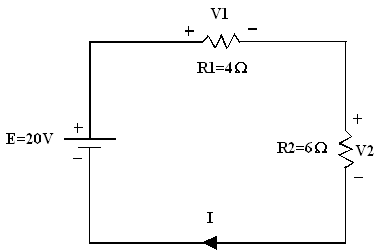
a) Calculer RT ;

b) Trouver I ;

c) Trouver V1 et V2 ;

d) Trouver la puissance fournie à R1 et R2 ;

e) Trouver la puissance débitée par la batterie et la comparer à la puissance dissipée par les résistances ;

f) Vérifier la loi des tensions de Kirchhoff. 

--------------------------------- 

a)  RT = R1 + R2 = 10 Ω 

b)  I = V / RT = 20 / 10 = 2 A 

c)  V1 = R1 x I = 4 x 2 = 8 volts 

V2 = R2 x I = 6 x 2 = 12 volts 

d) P1 = V1 x I = 8 x 2 = 16 watts 

P2 = V2 x I = 12 x 2 = 24 watts 

e)  P = E x I = 20 x 2 = 40 watts 

P1 + P2 = 16 + 24 = 40 watts   =>   P = P1 + P2 

f)  E - V1 - V2 = 0  =>  E = V1 + V2 soit 20 volts = 8 + 12 = 20 volts

4. Règle du diviseur de tension :

 

 

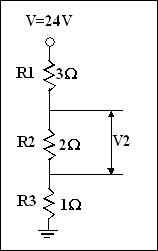
                   V                                     24

V2 = -------------------- x R2 = --------------- x 2 = 8 V

            R1 + R2 + R3                     3 + 2 + 1

 

 

 

Exercice 1 : calculez V2 et V’2 de la figure suivante :

 

----------------------------------- 

 

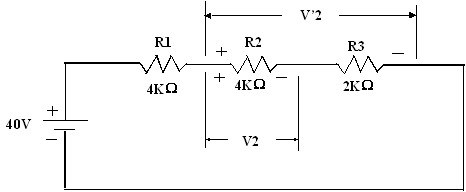
V2 = [40 / (R1 + R2 + R3)]x R2 = (40 / 10 K) x 4 K = 16 volts 

V’2 = [40 / (R1 + R2 + R3)] x (R2 + R3) = (40 / 10 K) x 6K = 24 volts 

Exercice 2 : soit la figure suivante :

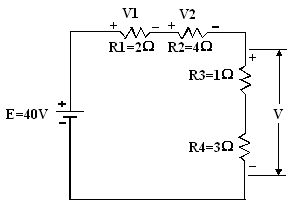
a)  Calculez V1

b)  Calculez V2

c)  Calculez V

d) Vérifiez la loi des tensions de Kirchhoff pour ce circuit

-----------------------------------

V1 = (40 / 10) x 2 = 8 volts 

V2 = (40 / 10) x 4 = 16 volts 

V = (40 / 10) x 4 = 16 volts 

E - V1 - V2 - V = 0   =>  E = V1 + V2 + V  soit 40 = 8 + 16 + 16    => 40 = 40 

5. Sources de tension en parallèle:

En courant continu, il faut éviter de monter des sources de tension en parallèle à moins que leurs caractéristiques ne soient identiques (même tension, même résistance interne).

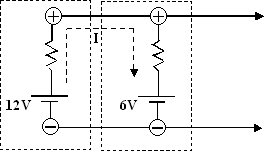
La batterie de 12 volts se déchargera dans la batterie de 6 volts. Par contre, des batteries de même tension sont parfois mises en parallèle si l’appel de courant d’une charge est plus grand que la capacité nominale d’une seule batterie.

6. Loi des courants de Kirchhoff :

La loi des courants de Kirchhoff est : la somme algébrique des courants qui arrivent à un nœud et qui en partent est nulle (un nœud étant le point de jonction de deux ou plusieurs branches). Autrement dit, la somme des courants qui arrivent à un nœud d’un circuit est égale à la somme des courants qui en partent.

 

  

 

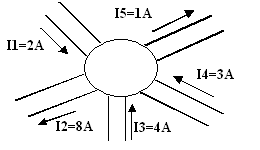
I1 + I3 + I4 = I2 + I5

2 + 4 + 3 = 8 + 1

9 = 9

 

 

Exercice1 : En utilisant la loi d’ohm, calculer le courant dans chacune des résistances des exercices 1, 2 et 3 précédents (paragraphe 1 : circuit parallèle). La tension d’alimentation est de 12 volts. 

---------------------------------- 

#1 :          IR1 = 12 / R1 = 12 / 2 = 6A 

                IR2 = 12 / R2 = 12 / 5 = 2.4A 

#2 :          IR1 = 12 / R1 = 12 / 3 = 4A 

                IR2 = 12 / R2 = 12 / 2.5 = 4.8A 

                IR3 = 12 / R3 = 12 / 8 = 1.5A 

#3 :          IR1 = IR2 = IR3 = 12 / R1 = 12 / 9 = 1.33A 

Exercice 2 : Pour le circuit suivant :

 

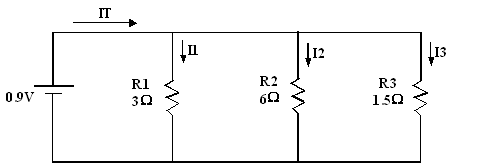
a) Déterminez la résistance totale du réseau ;

b) Calculez IT et le courant passant dans chacune des branches en parallèle ;

c) Calculez la puissance dissipée par chaque résistance et comparez la puissance fournie à la puissance dissipée. 

------------------------------------- 

  

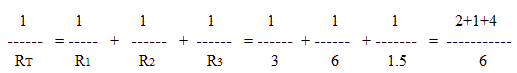
                6

RT   =   -------  =   0.857 Ω

               7

 

                   VT                  0.9

IT   =   -------   =   ---------   =   1.05 

            RT                 0.857

 

             VT                 0.9

I1   =   -------   =   ---------   =   0.3 A

             R1                 3

 

           VT               0.9

I2  =  -------   =   ---------   =   0.15 

           R2                  6

 

            VT               0.9

I3   =   -------   =   ---------   =   0.6 A

            R3              1.5 

P1 = 0.9 x 0.3 = 270 mW 

P2 = 0.9 x 0.15 = 135 mW 

P3 = 0.9 x 0.6 = 540 mW 

PT = 0.9 x 1.05 = 945 mW 

PT = P1 + P2 + P3 

945 mW = 270 mW + 135 mW + 540 mW 

945 mW = 945 mW 

Exercice 3 : Pour le circuit suivant

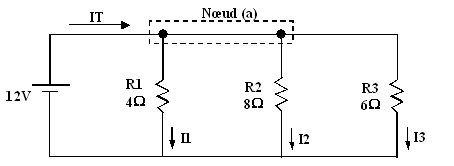
a) Déterminez la résistance totale du réseau ;

b) Calculez IT ;

c) Calculez le courant passant dans chacune des branches en parallèle ;

d) Vérifiez la loi des courants de Kirchhoff au nœud (a). 

------------------------------------- 

RT = 1.846 Ω 

IT = 6.49 A = 6.5 A 

I1 = 3 A,  I2 = 1.5 A,  I3 = 2 A, IT = 6.5 A = I1 + I2 + I3 = 3 + 1.5 + 2 = 6.5 A 

7. Règle du diviseur de courant :

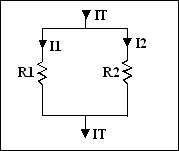
V  =  RT x IT 

              V              RT x IT                R2

I1`  =   -------   =   ----------   =   -----------      x I             

              R1              R1                   R1 + R2  

 

              V              RT x IT             R1

I2   =   --------   =  ----------   =   -------------     x I

              R2                  R2               R1 + R2

 

Exercice 1: Calculer les courants I1 et I2 du circuit suivant en utilisant la règle du diviseur de courant.

 

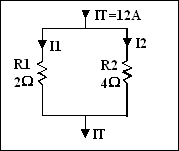
                     R2

I1   =   ---------   x   IT

              RT

 

4

I1  =   ---------   x   12   =   8 A

6

 

   R1

I2   =   ---------   x   IT

   RT

 

2

I2   =   ---------   x   12   =   4 A

6

 

Exercice 2: Déterminez le courant I1 dans le circuit suivant :

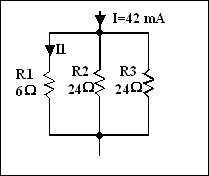
  R23

I1  =      ---------      x     IT

  RT

 

  12

I1  =       ---------      x     42 x 10^-3          =          28 mA

                 6 + 12

8. Court-circuit

Par élément court-circuité, on entend un élément aux bornes duquel est raccordée une branche de très faible résistance.

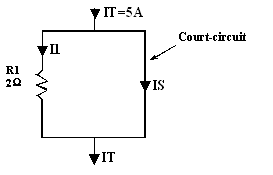
        2 x 5         10

IS = -------- = ------ = 5A

               2 + 0         2

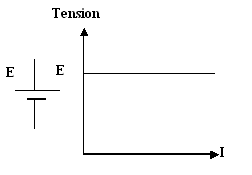
8. Source de tension

Une source à tension continue fournit idéalement une tension constante indépendamment des variations de l’appel de courant.

9. Source de courant

Une source à courant continu débite idéalement un courant d’intensité constante dans une charge, indépendamment des variations de tension aux bornes de la charge.

 

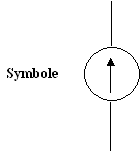
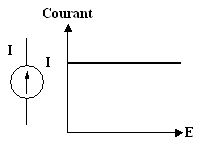
Exemple de source de courant de 1 mA :

 

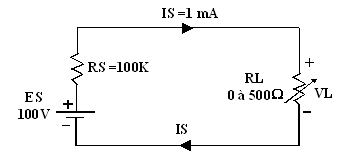
RL = 0     Is = Es / (Rs + RL) = 1 mA 

RL = 500Ω     Is = 0.995 mA   1 mA

 

 

 

 

Exercice 1: déterminez la tension VS et le courant I1 du circuit suivant :

 

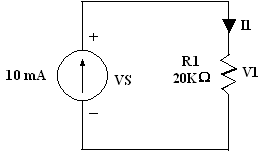
I1 = I = 10 mA 

VS = V1 = R1 x I1 = 20 K x 10 mA = 200 V 

 

 

  
Exercice 2 :

 

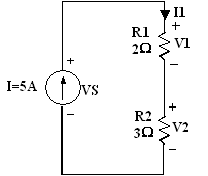
Calculer V1, V2 et VS 

  -------------------------------------------

V1 = R1 x I1 = R1 x I = 2 x 5 = 10 volts 

V2 = R2 x I2 = R2 x I = 3 x 5 = 15 volts 

VS - V1 - V2 = 0  =>  VS = V1 + V2 = 10 + 15 = 25 volts 

 

 

Exercice 3 :

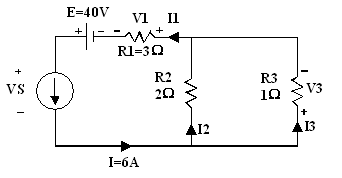
Calculer I2 ainsi que les tensions V3, V1 et VS 

                   ---------------------------------------------- 

I2 = R3 x I / (R2 + R3) = 1 x 6 / (2 + 1) = 2 A 

V3 = R3 x I3 = R2 x I2 = 2 x 2 = 4 volts 

V1 = R1 x I1 = R1 x I = 3 x 6 = 18 volts 

VS - E + V1 + V3 = 0  =>  VS = E - V1 - V3 = 40 - 18 - 4 = 18 volts

 

 

11- Circuit mixte

À la figure suivante, les résistances R1 et R2 sont en parallèle et en série avec la résistance R3. C’est un montage mixte.

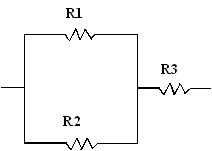
Exercice 1: Calculer les éléments inconnus de la figure suivante :

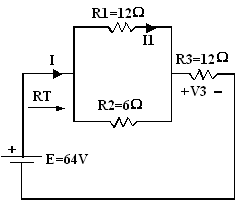
a) RT = (R1 // R2) + R3 = (12 // 6) + 12 = (12 x 6) / (12 + 6) + 12 = 4 + 12 = 16 Ω

b) E = RT x I  => I = E / RT = 64 / 16 = 4 A 

c) On applique le diviseur de courant : 

I1 = I x R2 / (R1 + R2) = 4 x 6 / (6 + 12) = 24 / 18 = 1.33 A 

d) On applique le diviseur de tension : 

E / RT = V3 / R3  =>  V3 = (R3 / RT) x E = (12 / 16) x 64 = 48 V

Exercice 2 : calculer I, V4 et Vab

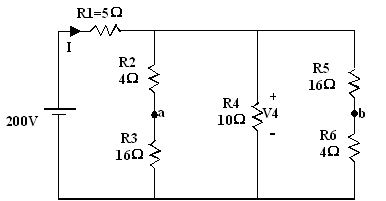
a) RT = [(R5 + R6) // R4 // (R2 + R3)] + R1 = (20 // 10 // 20) + 5 = 5 + 5 = 10 Ω

E = RT x I  =>  I = E / RT = 200 / 10 = 20 A

b) V4 = E - V1 = E - R1 x I = 200 - (5 x 20) = 200 - 100 = 100 volts 

c) Vab = Va - Vb 

V4 / (R2 + R3) = Va / R3 => 

Va = (R3 / R2 +R3) x V4 = (16 / 4 + 16) x 100 = 80 volts 

V4 / (R5 + R6) = Vb / R6 =>  

Vb = (R6 / R5 + R6) x V4 = (4 / 16 + 4) x 100 = 20 volts 

D’où Vab = Va - Vb = 80 - 20 = 60 volts

 

 

12- Théorème de superposition

            - Un court-circuit pour une source de tension

            - Un circuit ouvert pour une source de courant

Exemple 1 : déterminer le courant I1 dans le circuit ci-dessous.

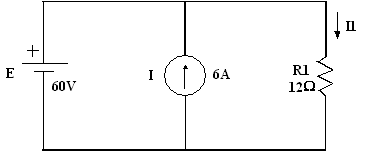
On considère une source à la fois. Courant dans R1 dû à la source de courant :

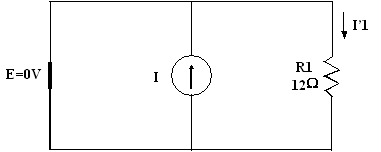
Courant dans R1 dû à la source de tension :

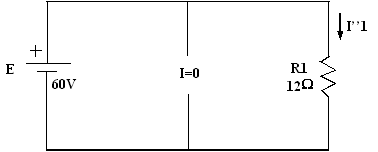
I"1 = 60 / 12 = 5 A

Le courant dans la résistance R1 est la somme de I’1 et I"1 soit I1 = I’1 + I"1 = 0 + 5 = 5 A

Exemple 2 : Déterminer le courant I3 traversant la résistance R3

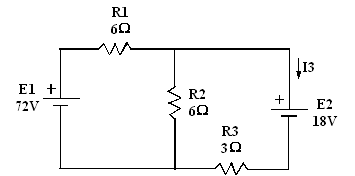
On considère une source à la fois.

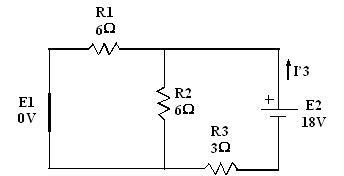
I’3 = I TOTAL = 18 / 6 = 3A

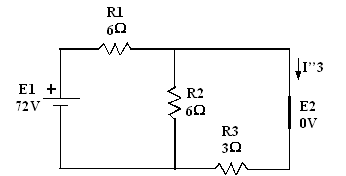
R TOTAL = 6 + 2 = 8Ω

I TOTAL = 72/8 = 9A

I"3 = (I x 6) / 3 = 6A

I3 = I"3 - I’3 = 6 - 3 = 3A (observer le sens du courant dans les deux figures précédentes).

 

 

13- La résistance variable

1. La codification des résistances variables

La codification de la valeur des résistances variables est effectuée de l'une ou l'autre des façons suivantes :

a) La valeur ohmique de la résistance fixe est directement inscrite en clair sur le boîtier : par exemple 100R, 500R, 1K, 10K, 1M, etc.

b) La valeur ohmique de la résistance fixe est codée numériquement sur le boîtier et s'interprète de la façon suivante : les deux premiers chiffres sont significatifs et le troisième chiffre indique le nombre de zéros à ajouter à ces chiffres significatifs. Par exemple :

500 = 50 Ω

502 = 5000 = 5K

503 = 50000 = 50K

2. Les potentiomètres de type PC MOUNT

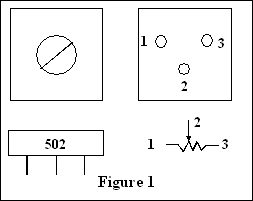
Le potentiomètre est composé d'une résistance fixe et d'un curseur se déplaçant sur cette dernière. La figure 1 vous présente une vue de côté, du dessus et du dessous d'un potentiomètre du même type (PC MOUNT). Le quatrième élément de cette figure représente le symbole graphique du potentiomètre. On y voit clairement que l'accès à la résistance fixe se fait par les bornes 1 et 3 tandis que l'accès au curseur est assuré par la borne 2.

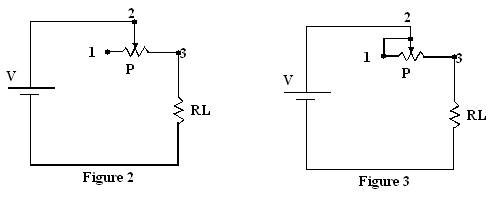
3. Le montage en rhéostat

Le montage en rhéostat fait véritablement appel à la notion de "résistance variable". Les figures 2 et 3 présentent deux façons de brancher la résistance variable en rhéostat ; la méthode illustrée à la figure 3 est préférable car elle évite de laisser flottante une des broches du potentiomètre.

4. Le montage en potentiomètre

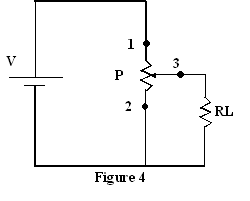
Contrairement au montage en rhéostat, dans le montage en potentiomètre, la résistance variable est parallèle à la source de tension. C’est ce type de montage qui est utilisé dans le réglage de volume des appareils audio.

 

14- Les condensateurs

 

Introduction

Champ électrique

Capacité

Rigidité diélectrique

Condensateurs en série

Condensateurs en parallèle

Charge d'un condensateur

Décharge d'un condensateur

Types de condensateurs

Codification de la tolérance

Codification du type de diélectrique

 

1.      Introduction : contrairement à la résistance, il ne dissipe pas d’énergie mais il l’emmagasine sous une forme telle qu’elle peut être restituée au circuit.

 

2.      Le champ électrique : il existe une force d’attraction ou de répulsion entre deux corps électrisés. Le champ électrique est représenté par des lignes de forces.

 

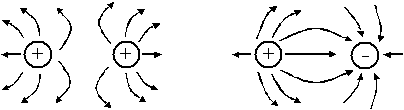
3.      Capacité

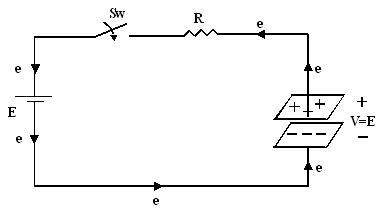
Nous avons raccordé deux plaques conductrices parallèles à une source de tension au moyen d’un circuit comprenant une résistance et un interrupteur, une couche d’air sépare les deux plaques. Des plaques ainsi montées portent le nom d’armatures. Si au départ les armatures étaient non électrisées et que l’interrupteur soit ouvert, il n’existe aucune charge positive ou négative sur l’une ou l’autre des armatures. Mais dès que l’interrupteur est fermé, des électrons passent de l’armature supérieure à la borne positive de la batterie en traversant la résistance. Ce déplacement d’électrons crée une charge nette positive sur l’armature supérieure. Par ailleurs, la borne négative repousse des électrons qui s’accumulent sur l’armature inférieure ; le nombre d’électrons passant à cette armature en une période de temps donné est égal au nombre d’électrons qui quittent l’armature supérieure. Ce transfert d’électrons se poursuit tant que la d.d.p. entre les armatures parallèles n’est pas égale à la f.e.m. de la batterie.

Un tel montage de deux armatures parallèles séparées par un matériau isolant (dans ce cas particulier l’air) constitue un condensateur simple.

La capacité est la mesure de l’aptitude d’un condensateur à emmagasiner des charges sur ses armatures.

La capacité d’un condensateur est de 1 Farad (en l’honneur de Michael Faraday = Physicien et Chimiste Anglais 1791-1867) si une ddp de 1 volt entre ses armatures y dépose une charge de 1 coulomb.

         Q

C = -----

         V

 

C en Farad (F)

Q en Coulomb (C)

V en Volt (V)

Le Farad est toutefois une unité trop grande pour être commode dans la plupart des cas ; le microfarad (mF) et le picofarad (pF) sont donc habituellement employés.

Sans changer les armatures, on peut faire varier la capacité d’un condensateur, en intercalant entre celles-ci divers matériaux isolant (papier, mica -roche modifiée par la chaleur et la pression-volcanique-transparente-, céramique -terre cuite-, tantale -métal légèrement bleuté-, verre)

 

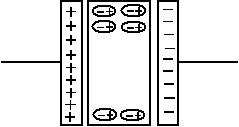
Grâce au diélectrique, des charges supplémentaires s’accumulent sur les armatures. Ces charges supplémentaires font augmenter la capacité du condensateur.

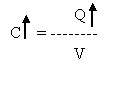
Le nombre de charges supplémentaires est fonction du matériau isolant utilisé.

La valeur de la capacité dépend d’une constante e propre à chaque diélectrique (vide, air, papier, caoutchouc, huile, verre), de l’aire des armatures (A) et de la distance (d) qui sépare les armatures. C est proportionnelle à ε et A et inversement proportionnelle à d.

εA

C   = --------

d

Quelques valeurs de ε : 1 pour le vide, 1.0006 pour l’air, 3 pour le caoutchouc, 4 pour l’huile, 5 pour le mica, 7.5 pour le verre et 1200 pour la céramique.

4.      Rigidité diélectrique : il existe une tension sous laquelle tout diélectrique  est percé par un courant. On dit alors que le diélectrique claque. Lorsque le diélectrique claque, le condensateur présente des caractéristiques semblables à celles d’un conducteur.

Matériau	Rigidité V/mil
Air	80
Huile	375
Céramique	1000
Papier	1200
Mica	1500
Verre	2000

1 mil = 0.001 po

5.      Condensateurs en série

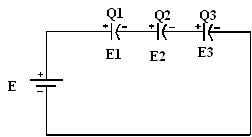
 Dans un montage série, la charge est la même pour chacun des condensateurs

QT = Q1 = Q2 = Q3 = Q

ET = E1 + E2 + E3

     

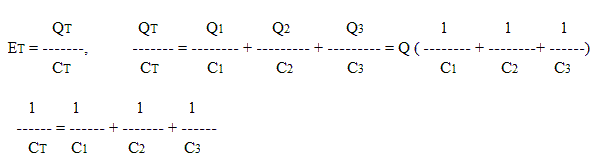
6.      Condensateurs en parallèle

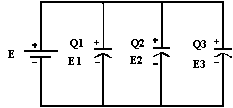
QT = Q1 + Q2 + Q3

ET = E1 = E2 = E3

QT = CT E = Q1 + Q2 + Q3

QT = CT E = C1 E + C2 E + C3 E =E (C1 + C2 + C3)

CT = C1 + C2 + C3

 

7.      Charge d’un condensateur

 

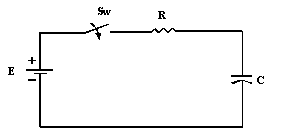
Une tension continue E est appliquée au condensateur de capacité C en série avec la résistance R. Le temps que prendra le condensateur à se charger dépend uniquement des valeurs de R et de C.

On définit une constante de temps τ = RC qui servira à la mesure du temps de charge du condensateur. τ (Tau) s’exprime en secondes. En effet :

τ = RC avec R = E / I et C = Q / V

R  => Volt / Ampère = Volt x seconde/Coulomb 

C  => Coulomb / Volt

R x C => (Volt x Seconde / Coulomb) x Coulomb / Volt = Seconde

 

§         Au départ le condensateur C est déchargé, l’interrupteur Sw est ouvert

§         Lorsqu’on ferme Sw, un courant I circule dans le circuit et vient charger C à travers la résistance R. Tout d’abord, ce courant aura une intensité maximale, qui va diminuer à mesure que le condensateur se charge. Après un temps relativement long (dépendant du produit RxC), le condensateur sera complètement chargé et alors le courant dans le circuit sera nul. À ce moment la tension aux bornes du condensateur est égale à la tension de la batterie.

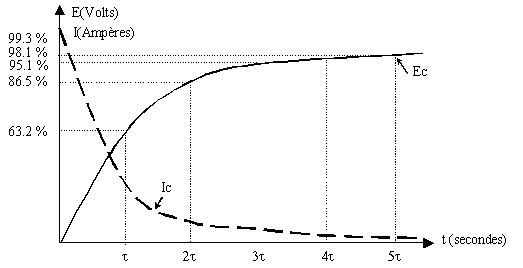
Le condensateur accumule sa plus grande charge durant la première constante de temps. On considère le condensateur complètement chargé au bout de 5 constantes de temps.

Exemple : R = 100 KΩ , C = 100 μF et E 100 volts

       τ = RC = 100 x 10³ x 100 x 10^-6 = 10 secondes

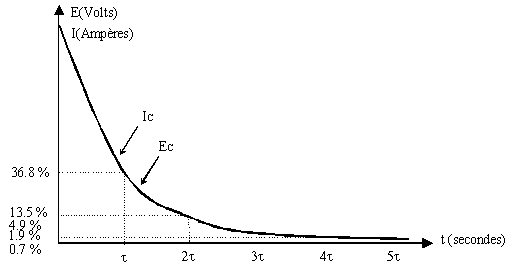
Au bout de 10 secondes, la tension EC atteindra 63.2 % de E soit EC = 63.2 volts

 

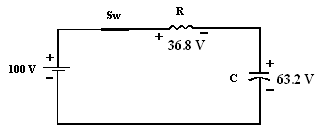
Le courant dans le circuit à ce moment là est I = E / R = 36.8 / 100 K = 368 μA

       2τ = 20 secondes EC = 86.5 V, ER = 13.5 V et I = 135 μA

       3τ = 30 secondes EC = 95.1 V, ER = 4.9 V et I = 49 μA

        4τ = 40 secondes EC = 98.1 V, ER = 1.9 V et I = 19 μA

        5τ = 50 secondes EC = 99.3 V, ER = 0.7 V et I = 7 μA

8.      Décharge d’un condensateur

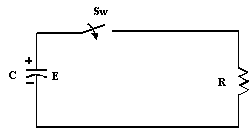
Au départ, le condensateur est chargé à une tension E

        Lorsqu’on ferme l’interrupteur Sw, un courant circule dans le circuit. Le condensateur perd la plus grande partie de sa charge durant la première constante de temps. Il est considéré comme complètement déchargé après 5τ.

Exercice 1

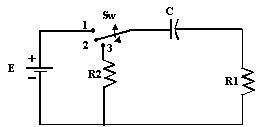
R1 = R2 =100KΩ, C = 0.05 μF et E = 10 volts

1)      Déterminer les constantes de temps de charge et de décharge du condensateur C

2)      Calculer le temps au bout duquel le condensateur sera complètement chargé

3)      À un temps déterminé la tension aux bornes du condensateur en charge est de 5.5 volts, calculer alors le courant IC.

-----------------------

Réponses :

 τ de charge = 5 ms

2τ de décharge = 10 ms

5τ = 25 ms

EC = 5.5 V => ER = 4.5 V => I = 45 μA

Exercice 2

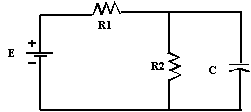
R1 = 4 Ω, R2 = 6 Ω, C = 20 μF et E = 24 volts

Calculer la charge et la tension aux bornes du condensateur C, s’il a été chargé à sa tension finale.

----------------------------

Réponses :

Ec = 24 x 8 / (4 +8) = 16 volts

Q = CxV = 320 μC 

Exercice 3

 

 

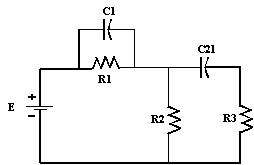
R1 = 2 Ω, R2 = 7 Ω, R3 = 8 Ω, C1 = 2 μF, C2 = 3 μF et E = 72 V

 Calculer la tension aux bornes des condensateurs C1 et C2 ainsi que leur charge si chacun d’eux est chargé à sa tension finale.

------------------------------

Réponses :

EC2 = 72 x 7 / (2+7) = 56 volts

EC1 = 72 x 2 / (2+7) = 16 volts

Q1 = C1 x E1 = 32 µC

Q2 = C2 x E2 = 168 μC

Exercice 4

 

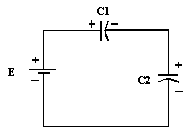
C1 = 100 μF, C2 = 22 μF et E = 10 volts

Calculer CT, Q1, Q2, E1 et E2

--------------------------------

Réponses :

CT = 18 μF

Q1 = Q2 =CT x E = 180 μC

E1 = Q / C1 = 1.8 V

E2 = Q / C2 = 8.2 V

Exercice 5

C1 = 800 µF, C2 = 60 μF, C3 = 1200 μF et E = 48 V

 

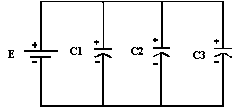
Calculer CT, Q1, Q2, Q3 et QT

--------------------------

Réponses

CT = C1 + C2 + C3 =2060 μF

Q1 = C1 x E = 38.4 mC

Q2 = C2 x E = 2.88 mC

Q3 = C3 x E = 57.6 mC

QT = Q1 + Q2 + Q3= 99 mC

Exercice 6

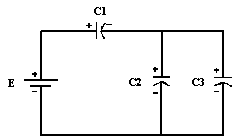
C1 = 3 μF, C2 = 4 µF, C3 = 2 μF et E = 120 V

Calculer Q1, Q2, Q3, E1, E2 et E3

---------------------------------

Réponses

CA = C1 // C2 = 6 μF

CT = 2 μF

QT = C x E = 240 μC

Q1 = 240 μC

E1 = Q1 / C1 = 80 V

E2 = E3 = 40 V

Q2 = C2 x E2 = 160 μC

Q3 = C3 x E3 = 80 μC

9.      Types de condensateurs

  Condensateurs au mica : on les utilise pour de faibles valeurs de capacités comprises entre 50 et 500 pF

  Condensateurs au papier : on les utilise pour des valeurs moyennes de capacités comprises entre 0.001 μF et 1 μF

   Condensateurs céramiques (terre cuite à haute température) : leurs valeurs sont comprises entre 1 et 500 pF (moins volumineux que les condensateurs au mica)

 

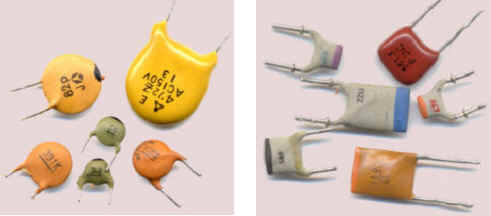
  Condensateurs électrolytiques (chimiques) : ils ont des valeurs comprises entre 1 et 10000 μF (capacités élevées pour de faibles dimensions).

 

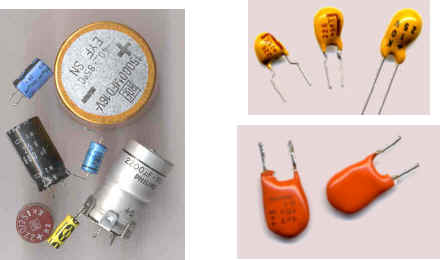
Ils sont constitués par deux électrodes en aluminium dont l’une est recouverte d’alumine (oxyde d’aluminium) qui est un très bon isolant. Les électrodes sont séparées par du papier spécial “Kraft” à la pâte de bois et le tout imprégné d’électrolyte (acide borique, phosphate ou carbonate). L’électrolyte peut être pâteux ou liquide.

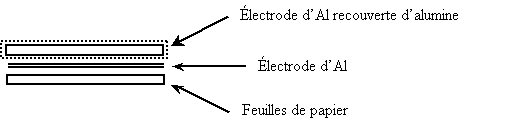
Le condensateur est ensuite placé dans un boîtier en aluminium et fermé.

Préparation de l’anode

 

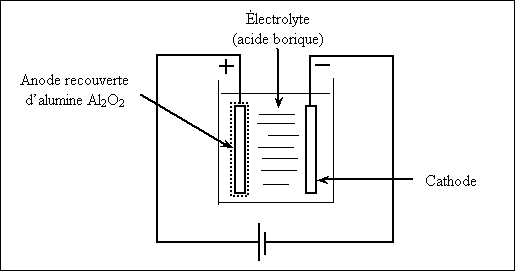
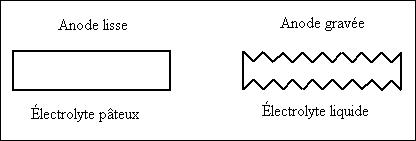
Quand on applique une tension continue pour former l’anode en cours de fabrication, le processus électrolytique accumule une mince couche d’oxyde d’aluminium à la jonction de l’électrode d’Al et de l’électrolyte. C’est ce film d’oxyde qui détermine la valeur de la capacité.

Il faut connecter les condensateurs électrolytiques de façon à ce que la tension appliquée maintienne l’électrode positive à un potentiel plus positif que l’électrode négative sinon le film d’oxyde ne se forme pas et il n’y a pas de capacité.

10.      Codification de la tolérance

Toutes les valeurs du tableau ne sont pas utilisées en pratique.

11.      Codification du type de diélectrique

 12.      Tension nominale des condensateurs : cette tension indique la ddp maximale que l’on peut appliquer entre les armatures sans percer le diélectrique.

13.      Code de couleur des condensateurs : les condensateurs au mica et les condensateurs céramiques tubulaires sont codés par couleur pour indiquer la valeur de leur capacité. Les valeurs sont toujours exprimées en pF. On utilise les mêmes couleurs que pour le codage des résistances. Ce type de condensateur n'est plus fabriqué mais on les rencontre très fréquemment dans les appareils datant des années 1970 à 1990. Les bagues de couleurs se lisent de haut en bas.

 

 Exemples :

Repère D de la photo : brun : 1 - premier chiffre significatif, vert : 5 - deuxième chiffre significatif, jaune : x10000 - multiplicateur, la capacité est de 150nF, blanc : 10% - tolérance,

marron : 100 V - tension de service en continu maximale

Repère E de la photo : brun - noir - jaune - noir – rouge, capacité : 100nF, tolérance 20%, tension maxi 250 volts

Repère F de la photo : brun - gris - orange - blanc – brun, capacité : 18nF, tolérance 10%, tension maxi 100 volts

Repère G de la photo : les bandes se lisent de bas en haut, brun - vert – rouge, capacité : 1,5nF

Repère H de la photo, brun - vert – rouge, capacité : 1,5nF

14.      Codage alphanumérique des condensateurs 

Il se présente sous trois formes :

  La codification en pF : elle consiste à inscrire la valeur sur le condensateur à l’aide de chiffres sans autre indication (le picofarad étant implicite). Cette codification fait appel à des nombres entiers seulement.

Exemple : 1500 J = 1500 pF ± 5 %, 680K = 680 pF ± 10 %

  La codification en pF suivie d’un multiplicateur : elle fait appel à des nombres de trois chiffres. Les deux premiers sont significatifs et sont associés à une valeur en pF. Quant au troisième chiffre, il désigne le nombre de zéros à ajouter aux chiffres significatifs, le zéro étant exclu.

Exemples :

Repère J de la photo : code : n27 = 0,27 nF, capacité : 270pF

(la bande violette est le coefficient de température : -750.10-6/°C)

Repère K de la photo : code : 224K 100V, capacité :220000pF (220nF) - 10% - 100 volts

Repère L de la photo : code : 473 KCK, capacité :47000pF (47nF) - fabricant KCK

Repère M de la photo : code : 104 KCK, capacité :10000pF (10nF) - fabricant KCK

 

  La codification en μF : elle consiste à inscrire la valeur directement sur le condensateur (le microfarad est implicite). Cette codification fait appel à des nombres fractionnaires.

Exemple : 0.01M = 0.01 μF± 20 %, 0.5J = 0.5 μF ± 5 %, 0.15K = 0.15 μF ± 10 %

 

Condensateur au tantale - Repère A sur la photo, Il est marqué : 226F, ce qui peut se traduire par : 2 : premier chiffre significatif, 2 : deuxième chiffre significatif, 6 : 6 zéros à ajouter aux deux premiers chiffres pour obtenir la capacité en pF qui est ici de 22 000 000 pF = 22μF. La lettre F indique une tolérance de ±1% (voir tableau ci-dessous)

Remarque : on trouve aussi le type de marquage suivant : 22u 25V qui indique une capacité de 22μF et une tension maxi de 25 volts

Condensateur à film plastique - Repère B sur la photo est marqué : .1 K 160V MKT ce qui signifie : capacité : 0,1μF , K : tolérance de ±10% (voir tableau ci-dessous), 160V : tension de service en continu maximale. MKT : type de diélectrique, ici du polyester (voir tableau ci-dessous)

Le repère C sur la photo est marqué : .1 K 100V MKT, capacité de 0.1μF ± 10 %, 100V de tension de service maximale.

 Exercices

            Donner la valeur nominale du condensateur ainsi que le pourcentage de tolérance pour chacun des codes suivants :

Code	Valeur	% d’erreur
101M	100pF	20
133J	13000pF	5
0.01J	0.01μF	5
471	470pF	20
472	4700pF	20
0.22K	0.22μF	10
3300±5	3300pF	5

 

              Donner le code approprié pour chacun des condensateurs suivants :

Valeur	Code
100nF	0.1 ou 104
0.1μF	0.1 ou 104
470nF	0.47 ou 474
470pF	470 ou 471
0.001µF	102
47nF	473
2200µF	2200mF ou 228