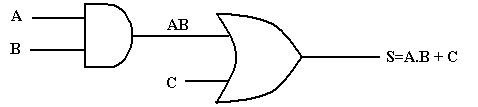
Tout circuit logique, quelle que soit sa complexité, peut être décrit au moyen des opérations booléennes « ET », « OU » et « NON » car ces portes sont des circuits élémentaires des systèmes numériques.

Exemple :

La sortie de la porte « ET » a pour expression A.B, cette combinaison est une entrée de la porte « OU » dont l’autre entrée est le signal C. Cette dernière a pour effet d’additionner logiquement ses entrées ce qui donne comme expression de sortie S = AB+C = C+AB.

L’ordre des termes dans une fonction « OU » n’a pas d’importance.

Parfois , il arrive qu’il y ait confusion sur l’opération d’une expression qui doit être effectuée en premier. A.B + C peut être interprété de deux façons :

      Où bien A.B est additionné logiquement (porte OU) avec C

      Où bien A est multiplié logiquement (porte ET) avec B+C

 Pour lever cette indétermination, il est convenu que dans une expression contenant des opérateurs « ET » et « OU », ce sont les opérateurs « ET » qui sont appliquées en premier sauf s’il y a des parenthèses ; dans ce cas il faut évaluer avant toute chose l’expression entre parenthèses.

 A . B + C est différent de A (B + C). Pour le confirmer, établissons les tables de vérité des deux expressions et comparons les sorties

 On constate en effet que les sorties des expressions AB+C et A(B+C) sont différentes.

 Exemple : Écrire l’expression algébrique du circuit suivant :

S = (A+B).C 

 Noter la parenthèse pour dire que A et B sont d’abord additionnés logiquement avant que leur somme ne soit multipliée logiquement avec C.

 Sans parenthèses, l’expression serait erronées A + B.C

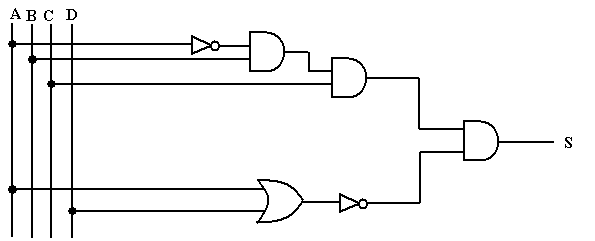
 Exercice 1 : Écrire l’expression algébrique du circuit suivant :

Exercice 2 : Remplacer la porte « OU » par la porte « ET » et les portes « ET » par des portes « OU » dans le circuit de l’exercice 1. Écrire ensuite la nouvelle expression de la sortie.

Exercice 3 : Quelle est le niveau logique de la sortie S du circuit de l’exercice 1 dans le cas où A=0, B=1, C=1 et D=1

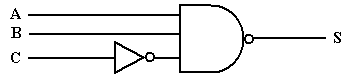
Exercice 4 : Déterminer le niveau de sortie du circuit suivant pour le cas où A=E=0 et B=C=D=1

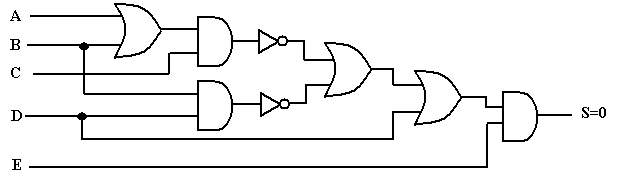
 Exercice 5 : Écrire l’expression logique de S. Trouver la valeur de S pour toutes les conditions possibles d’entrée et dresser la table de vérité.

Si l’opération d’un circuit est définie par une expression booléenne, il est possible de tracer directement un diagramme logique à partir de cette expression. Supposons qu’on veuille construire un circuit dont la sortie :

 Cette expression est constituée de trois termes :

qui sont additionnés logiquement. On déduit qu’il nous faut une porte « OU » à trois entrées auxquelles sont appliquées respectivement les signaux

Exercice 1 : Tracer le diagramme du circuit dont la sortie est :

 Exercice 2 : Tracer le diagramme du circuit dont la sortie est :

Exercice 3 : pour chacune des expressions suivantes, construisez le circuit logique correspondant :

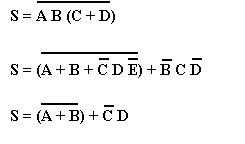
3.1.   Théorèmes pour une seule variable A

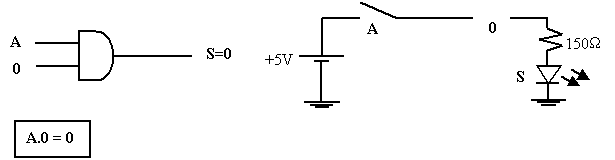
 Théorème 1 : la mise en fonction « ET » de toute variable avec 0 donne nécessairement 0 car l’opération « ET » est équivalente à la multiplication ordinaire.

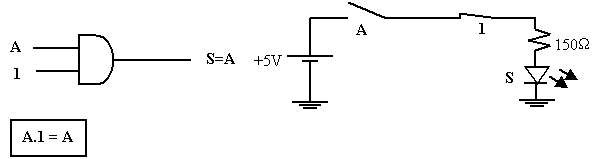
Théorème 2 : la mise en fonction « ET » d’une variable A avec 1 donne toujours A. Ce qui évident si on compare avec la multiplication ordinaire.

Théorème 3 : la mise en fonction « ET » de la variable A avec elle-même donne toujours A

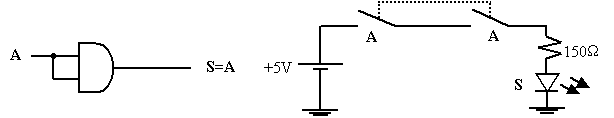
On examine les diverses possibilités :

 Théorème 4 : la mise en fonction « ET » de la variable A avec son complément donne 0

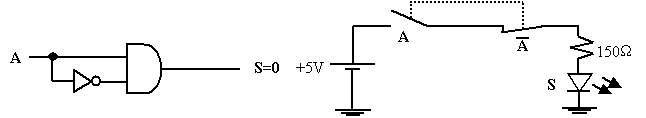
La démonstration est analogue à la précédente

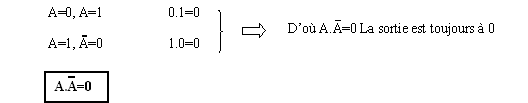
Théorème 5 : le fait d’additionner un 0 à n’importe quelle valeur ne change rien.

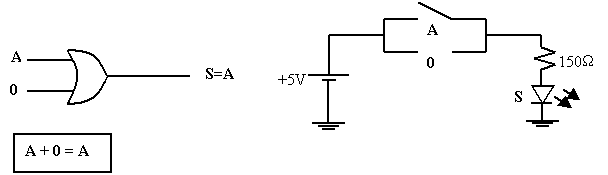
 Théorème 6 : la mise en fonction « OU » d’une variable A avec 1 donne toujours 1.

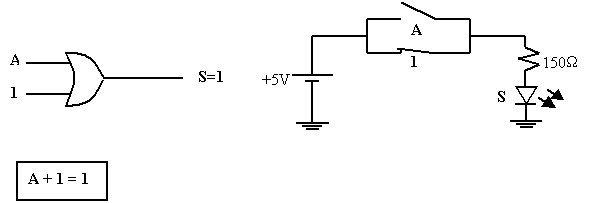
Théorème 7 : la mise en fonction « OU » d’une variable A avec elle-même donne toujours A.

On examine les deux possibilités :

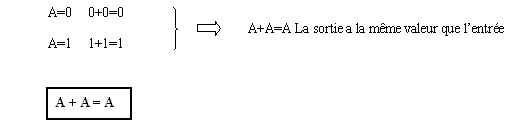
 Théorème 8 : la mise en fonction « OU » d’une variable A avec son complément donne toujours 1.

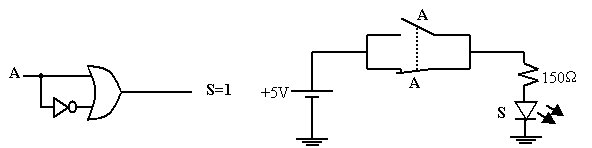
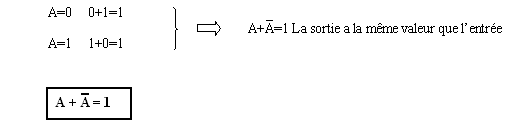
 3.2.   Théorèmes pour plusieurs variables

Théorème 9 : L’opération « OU » est une loi de composition commutative, c’est-à-dire que l’ordre de l’addition de deux ou plusieurs variables n’a pas d’importance, que le résultat reste le même.

Théorème 10 : L’opération « ET » comme l’opération « OU » est une loi de composition commutative, donc l’ordre de la multiplication de deux ou plusieurs variables n’a pas d’importance, le résultat reste le même.

Théorème 11 : « OU » est une loi de composition associative, qui indique que l’on peut grouper, comme l’on veut, les variables dans une opération d’addition.

Théorème 12 : « ET » est une loi de composition associative, qui indique que l’on peut grouper, comme l’on veut, les variables dans une opération de multiplication

Théorème 13 : La multiplication logique est distributive par rapport à l’addition logique, c’est-à-dire que l’on peut développer une expression en la multipliant  terme à terme comme dans l’algèbre ordinaire. Ce théorème démontre également que l’on peut mettre en facteur une expression. On veut dire par là que si nous avons une somme de termes, chacun renfermant une variable commune, il est possible de mettre cette variable en facteur.

Théorème 14 : c’est un théorème d’absorption A + AB =A. En effet A + AB possède deux termes comprenant chacun la variable A que l’on peut mettre en facteur :

 A + AB = A(1 + B) et 1+B =1 (voir théorème 6)   => A + AB = A . 1 = A

 On peut également le vérifier en considérant les quatre cas possibles :

 1^e cas : A =0, B=0   => A + AB = 0 + 0.0 = 0

 2^e cas : A =0, B=1   => A + AB = 0 + 0.1 = 0

3^e cas : A =1, B=0   =>  A + AB = 1 + 1.0 = 1

 4^e cas : A =1, B=1   =>    A + AB = 1 + 1.1 = 1

 On constate que A + AB prend la même valeur que la variable A

Les théorèmes de De Morgan se révèlent d’une grande utilité pour simplifier des expressions comprenant des sommes ou des produits de variables complémentées. Voici ces deux théorèmes :

 Théorème 16 : la somme logique complémentée de deux variables est égale au produit logique des compléments de ces deux variables.

Théorème 17 : le produit logique complémenté de deux variables est égal à la somme logique des compléments de ces deux variables.

Ces théorèmes sont aussi vrais pour les cas où A et B sont des expressions comprenant plusieurs variables.

Les théorèmes de De Morgan permettent de couper une barre de complémentation à n’importe quel point d’une expression et de changer l’opérateur en ce point par l’autre (changer le signe (+) par le signe (.) et vice versa). Cette démarche est répétée jusqu’à ce que l’expression ne soit plus formée que de variables simples.

Conséquences des théorèmes de De Morgan

Exercice 1 : Réaliser avec une porte « NON-ET » et un inverseur, un circuit ayant comme expression

Inversons deux fois l’expression, une double complémentation ne modifie en rien la valeur logique.

À l’aide du théorème de De Morgan, fractionnons la barre de surlignement inférieure :

Exercice 2 : Construire en utilisant seulement  une porte « NON-OU » et un inverseur, un circuit ayant comme expression de sortie :

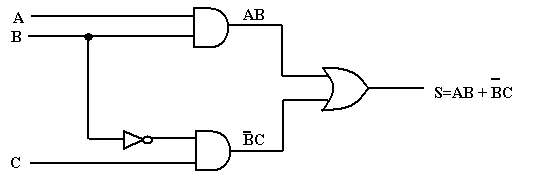
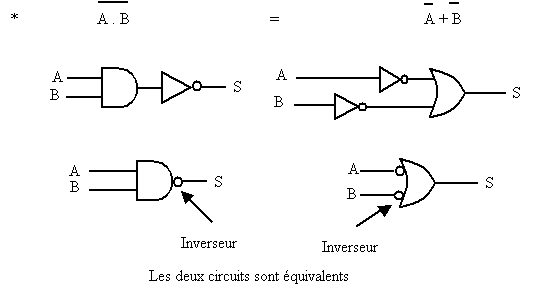
Exemple : les deux circuits suivants sont équivalents

Les méthodes de simplification et de conception de circuits logiques exigent que l’on exprime les équations logiques sous la forme d’une somme de produit.

Exemple :

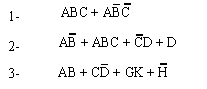
Chaque terme comprend une ou plusieurs variables sous forme normale ou complémentée.

Les théorèmes de l’algèbre booléenne sont toujours utilisés pour simplifier l’expression d’un circuit logique. Dans la simplification logique, il y a toujours deux étapes essentielles :

a)      La transformation par applications successives des théorèmes de De Morgan et par multiplication de termes de l’expression pour obtenir une somme de produits

Exemple :

 b) La vérification de chaque produit pour trouver les variables communes, puis la mise en facteur de ces dernières, le cas échéant. Quand une simplification est possible, la mise en facteur permet d’éliminer un ou plusieurs termes.

Exemple :

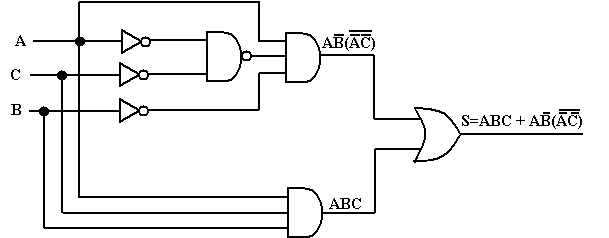
Solution : la première étape consiste à établir l’expression de la sortie. Cette expression est :

Quand on a l’expression, on la décompose au moyen des théorèmes de De Morgan, ensuite on multiplie tous les termes :

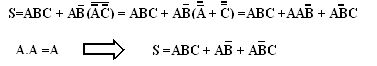
Maintenant que nous avons la somme de produits, voyons les variables communes dans les divers termes en vue de les mettre en facteur.

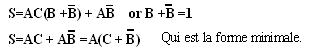
Exercice 2 : simplifiez l’expression

 1^e méthode :

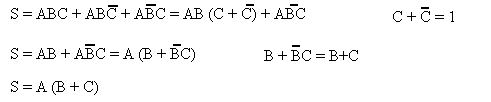
2^e méthode :

Exercice 3 : simplifiez l’expression

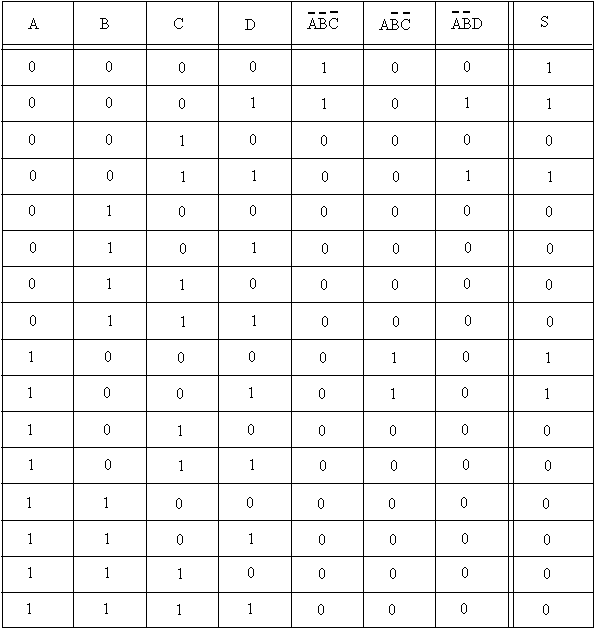
L’expression pour la sortie S découle de la table de vérité et se présente sous la forme de produits. Soit la table de vérité suivante :

 Procédure générale :

a)      Pour chaque cas de la table qui donne 1 en sortie, on écrit le produit logique « ET » qui lui correspond.

b)      On doit retrouver toutes les variables d’entrée dans chaque terme « ET » soit sous forme directe soit sous forme complémentée.

c)      On additionne logiquement ensuite tous les produits logiques constitués, ce qui donne l’expression définitive de la sortie.

Dès que l’expression de la sortie est établie sous la forme d’une somme de produits à partir de la table de vérité, il est alors facile de construire le circuit au moyen de portes « ET », « OU » et « NON ».

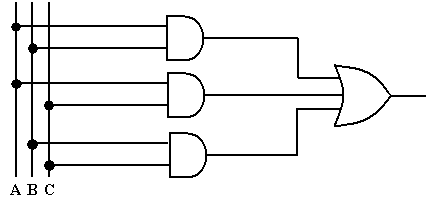
Exemple : concevez un circuit logique formé de trois entrées A, B et C dont la sortie est à 1 quand une majorité des entrées sont à 1.

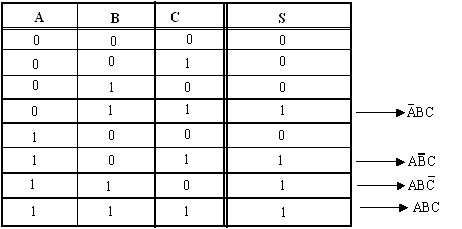
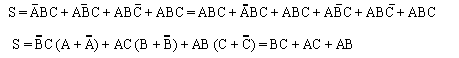
Le diagramme de Karnaugh est un outil graphique qui permet de simplifier de manière méthodique une équation logique

 3.1.   Forme du diagramme de Karnaugh : le diagramme de Karnaugh comme la table de vérité est un instrument qui met en évidence les rapports entre les entrées logiques et la sortie recherchée.

Diagramme de Karnaugh pour deux variables :

Diagramme de Karnaugh pour trois variables

Diagramme de Karnaugh pour quatre variables

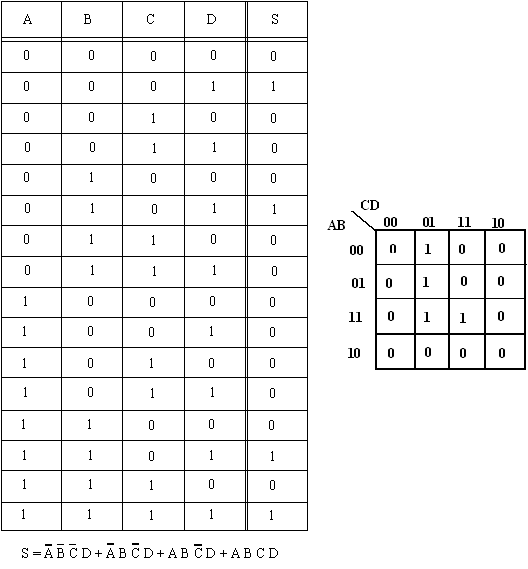
 a)      La table de vérité donne la valeur de S pour chacune des combinaisons des valeurs d’entrée ; par contre, le diagramme de Karnaugh organise l’information de manière différente. Chaque ligne de la table de vérité correspond à un carré du diagramme de Karnaugh.

b)      Les carrés d’un diagramme de Karnaugh sont désignés de manière que les carrés adjacents soit horizontalement, soit verticalement n’aient qu’une variable qui soit différente.

AB

00

01

11

10 

La case du haut est adjacente de la case du bas. De même la case de la colonne de gauche est adjacente à la case de la colonne droite.

CD = 00   01   11   10

c)      Pour que les cases adjacentes verticalement et horizontalement ne différent que d’une variable, il faut désigner les cases selon le code « GRAY »

 d) Dès qu’un diagramme est garni de 1 et de 0, il s’agit, pour obtenir S sous la forme d’une somme de produits, d’additionner logiquement les carrés qui renferment un 1.

 3.2.   Réunion : il est possible de simplifier l’expression de sortie S en combinant selon des règles précises les cases qui contiennent des 1. Ce processus est appelé réunion.

 a)      Réunion de doublets (de paires)

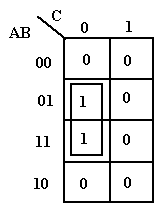
Pour ce regroupement, les variables qui sont semblables (normales ou complémentées) forment l’équation de la sortie soit :

Exemple 2 :

Le principe est le même que pour un doublet de 1 adjacents horizontalement

 Exemple 3 :

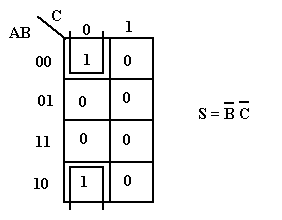
Exemple 4 :

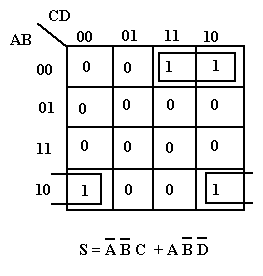
La réunion d’un doublet de 1 adjacents dans un diagramme de Karnaugh élimine la variable qui est à la fois complémentée et non complémentée.

Retour au début

Sommaire

Accueil