Les filtres passe-bas

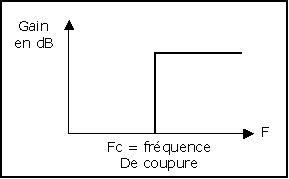
Leur diagramme gain-fréquence de réponse idéale est semblable à celui de la figure suivante.

Jusqu’à la fréquence Fc dite fréquence de coupure, le signal passe à travers le filtre. À cette fréquence, il y a coupure et aucun signal de fréquence supérieure à Fc ne traverse le filtre.

Les filtres passe-haut

Dans ce cas, le signal de fréquence inférieure à Fc est coupé et celui de fréquence supérieure à Fc n’est pas atténué.

Les filtres coupe-bande ou éliminateurs de bande

Ces filtres sont des combinaisons (parallèles) de filtres passe-bas et de filtres passe-haut. Tout signal de bande de fréquence comprise entre Fb (fréquence de coupure basse) et Fh (fréquence de coupure haute) est éliminé tandis que tout signal d’une autre fréquence est transmis.

Les filtres passe-bande ou à bande passante

Ces filtres sont des combinaisons (séries) de filtres passe-haut et de filtres passe-bas. Dans ce cas, seule la bande de fréquence comprise entre Fb (fréquence de coupure basse) et Fh (fréquence de coupure haute) est transmise. Les autres fréquences sont rejetées.

1.1. Rappel sur le décibel

L’amplification est définie comme étant le rapport d’une grandeur de sortie sur une grandeur d’entrée.

Amplification en puissance A_P = P_OUT/P_IN

Amplification en tension A_V = V_OUT/V_IN

Amplification en courant A_I = I_OUT/I_IN

Il est plus commode de prendre une échelle logarithmique, ce qui rétrécit l’étendue de la variation : ainsi, si un rapport varie de 1 à 1000 000, son logarithme décimal varie de 0 à 6.

Le Bel (symbole B) est par définition le logarithme décimal de l’amplification en puissance.

A_P (Bels) = Log A_P

1 Bel = Log 10 alors si  le gain A_P = 10   =>  A_P (B) = 1

Exemples :

A_P = 10 000   =>  A_P (B) = Log 10 000 = 4 B

A_P = 20 000   =>  A_P (B) = Log 20 000 = 4.3 B

Afin de réduire l’emploi des nombres décimaux, le gain en puissance est exprimé le plus souvent en décibels (dB).

1 Bel = 10 décibels, donc     A_P (dB) = 10 Log A_P

Exemples :

A_P = 10 000  =>  A_P (dB) = 10 Log 10 000 = 40 dB

A_P = 20 000   =>  A_P (dB) = 10 Log 20 000 = 43 dB

Gain en tension exprimé en décibels :

P = V² / R   =>  P_OUT = V²_OUT/R, P_IN = V²_IN/R

A_P = P_OUT/P_IN = V²_OUT/V²_IN = (V_OUT/V_IN)²

Le gain sera cette fois calculé en fonction des tensions, on le notera alors :

A_V (dB) = 10 Log (V_OUT/V_IN)² . Comme Log X² = 2 Log X  alors :

A_V (dB) = 10 x 2 Log V_OUT/V_IN = 20 log V_OUT/V_IN

Gain en courant exprimé en décibels :

De la même façon que précédemment, P=RI²  =>  P_OUT =RI²_OUT, P_IN=RI²_IN

Comme A_I = I_OUT/I_IN, alors              A_I (dB) = 20 Log I_OUT/I_IN

Décibels négatifs : 

Si la grandeur de sortie est plus petite que la grandeur d’entrée, il y a atténuation ou affaiblissement et le gain en décibels est alors négatif.

Exemple : P_IN = 3 W, P_OUT = 1.5 W

P_OUT/P_IN = 1.5/3 = 0.5   =>  A_P (dB) = 10 Log 0.5 = -3 dB

L’exemple suivant montre la commodité de l’échelle logarithmique :

On parle devant un microphone qui fournit un signal de 30 mV. Ce signal passe dans un préamplificateur qui fournit un signal ligne de 1 à 2 volts. Ce signal attaque un amplificateur de puissance (1000W/4Ω). À sa sortie, on pourra mesurer environ 63 volts, ce qui suffira à faire bouger la membrane d’un haut-parleur pour déranger tout le voisinage.

En calculant le facteur d’amplification "Av" de cette chaîne, on obtient :

Av = VOUT / VIN = 63 / 0.03 = 2100

On peut pousser encore plus loin. Un amplificateur de 2000 Watts sous 8 ohms délivre 126 volts au haut-parleur. En partant d’un très faible signal de l’ordre de 10 mV capté par un microphone électrostatique, l’amplification "Av" est de :

Av = VOUT / VIN = 126 / 0.01 = 12600

Exprimés en décibels, ces gains sont de :

Av = 2100   =>  Av (dB) = 20 log 2100 = 66.4 dB

Av= 12600   =>  Av (dB) = 20 log 12600 = 82 dB

En résumé, le DÉCIBEL rétrécit l’étendue de la variation : ainsi, si un rapport varie de 1 à 1000 000, son logarithme décimal varie de 0 à 6, l’amplification en tension quant à elle varie de 0 à 120 dB. Ceci est le premier avantage de l’utilisation du décibel.

Le deuxième avantage est que l’on peut facilement additionner les facteurs d’amplification d’une chaîne audio ou vidéo. Ceci découle de la propriété des logarithmes : Log (A1 x A2) = Log A1 + Log A2

Exemple

On peut de la même manière exprimer en décibel aussi bien le gain en puissance que le gain en courant.

AP (dB) = 10 Log (POUT / PIN)

AI (dB) = 20 Log (IOUT / IIN)

Les amplificateurs de sonorisation et les amplificateurs d’antennes ont généralement un gain de 26 dB à 32 dB ce qui signifie qu’ils augmentent la valeur de la tension de 20 à 40 fois respectivement.

Puissance versus tension :

La puissance P = V² / R, ce qui signifie que :

      Si R = 50Ω, V_IN = 1V, V_OUT = 1V   =>  Av = 1, P_OUT = 20mW

On amplifie le signal de 1.414 = 2^1/2, la tension V_OUT est alors de 1.414   =>  A_V = 1.414, P_OUT = 40mW. On constate que la puissance a doublé. Noter que 1.414 = 1/0.707

Le gain A_V exprimé en décibel est alors de A_V (dB) 20 Log 1.414 = +3dB.

      Si la tension double soit V_OUT = 2V, A_V = 2   =>  P_OUT = (2)² / 50 = 80mW, AV (dB) = 20 Log 2 = +6 dB, la puissance quadruple.

Oreille humaine :

Le volume du son (pression acoustique) est lui aussi converti de façon logarithmique et chiffré en décibels.

Physiquement la pression acoustique est mesurée en Pascal ou Newton/m². L’étendue du son du plus faible au plus fort va d’environ 0.00002 Pa ou N/m² à 1500 Pa ou N/m². Pour éviter des chiffres trop compliqués, on a converti ces nombres en dB, la référence ou le 0 dB étant le 0.00002 Pa.

Aux alentours de 130 à 140 dB, l’oreille commence à rendre l’âme.

Un bruit de fond correspond à : 40 à 50 dB

Une conversation normale : 60 à 80 dB

Les sons médiums (1Khz à 4Khz) sont perçus plus forts que les aigus et les graves. Moins le volume est fort, plus se creusera cette différence de perception. Sur certains systèmes de son haute fidélité, on retrouve un réglage LOUDNESS, qui justement relève le niveau des aigus et des basses pour parer à ce déséquilibre à bas niveau.

Décade et octave :

Une décade est l’espace entre deux fréquences dont le rapport est de 10 alors qu’une octave est l’intervalle entre deux fréquences dont l’une est le double de l’autre.

Exemple :

Dans la suite des fréquences suivantes : 10Hz, 100Hz, 1Khz, 10Khz, 100 Khz, l’espace entre deux fréquences successives est d’une décade.

Dans la suite des fréquences suivantes : 10Hz, 20Hz, 40Hz, 80Hz, 160Hz, l’espace entre deux fréquences successives est d’une octave.

Le terme – 20 dB / décade signifie que le gain en tension diminue de 10 fois sa valeur lorsque la fréquence augmente de 10 fois sa valeur.

20 log (VOUT/VIN) = -20    =>   log (VOUT/VIN) = -1   =>  (VOUT/VIN) = shift log (-1) = 10^-1 = 0.1 ou VOUT = VIN / 10

Le terme – 6 dB / octave signifie que le gain en tension diminue de 2 fois sa valeur lorsque la fréquence augmente de 2 fois sa valeur.

20 log (VOUT/VIN) = -6   =>  log (VOUT/VIN) = -0.3   =>  (VOUT/VIN) = shift log (-0.3) = 10^-0.3 = 0.5 ou VOUT = VIN / 2

1.2. Les filtres passifs

Ils sont construits avec des résistances, des bobines et des condensateurs et n’ont pas besoin de polarisation. Pour se familiariser avec le filtrage et la réponse en fréquence des filtres, nous allons étudier les différents types de filtres passifs.

a) Filtre passe-bas

Pour VIN =20 et R2 prenant successivement les valeurs 10K, 5K, 1K, 500Ω, 100Ω, 50Ω, 25Ω et 15Ω, Calculons VOUT

On remarque que la tension de sortie diminue au fur et à mesure que la résistance diminue. En alternatif, si on remplace la résistance R2 par un composant dont la réactance diminue avec l’augmentation de la fréquence, on obtient un filtre RC. Le condensateur est le composant qui présente cette caractéristique.

La réactance du condensateur est inversement proportionnelle à la fréquence :

                   

 Xc = 1 /2πFC
                                   

Voyons les différentes valeurs que prend la réactance d’un condensateur de 16 mF en fonction de la fréquence du signal qui lui est appliqué (voir tableau ci-après).

Avec une tension d’entrée de 20 volts et une résistance de 10 Ω en série avec le condensateur, les tensions aux bornes du condensateur C sont les suivantes :

F (Hz)	XC (Ω)	Z (Ω)	VC (V)	VC / V	VC / V (dB)
1	9947	9947	20	1	0
10	994.7	994.7	20	1	0
100	99.5	100	19.9	0.995	- 0.04
200	49.74	50.74	19.6	0.98	- 0.175
400	24.87	26.8	18.56	0.928	- 0.65
994.7	10	14.14	14.14	0.707	- 3
10K	0.99	10.05	1.97	0.0985	- 20
20K	0.497	10.01	0.99	0.049	- 26
100K	0.099	10	0.2	0.01	- 40

Supposons qu’on applique cette tension Vc à une résistance pure de 10 Ω et calculons les puissances dissipées dans celle-ci à la fréquence de 10 Hz puis à la fréquence de résonance 994.7 Hz : 

À 10 Hz V1 = Vc = 20 volts

À 994.7 Hz, V2 = 0.707 x Vc = 14.14 volts

P1 = V1²/R = 20²/10 = 40 W

P2 = V2²/R = 14.14²/10 = 20 W

P2 / P1 = 20 / 40 = 0.5 soit 50 %

Le signal a perdu 50% de sa puissance. La fréquence de coupure de ce filtre est bien de 994.7 Hz.

On remarque que ce filtre coupe les fréquences hautes et laisse passer les fréquences basses. La coupure se produit lorsque R = XC

R = XC   => R = 1 / 2πFC   =>  FC = 1 / 2πRC = 1 / 2π x 10 x 16 x 10^-6 = 994.7 Hz

L’atténuation de ce filtre est de :

- 6 dB par octave 

Exemple : prenons l’octave 10 Khz – 20 Khz du tableau précédent :

À 10 Khz, Vc / E = -20 dB

À 20 Khz, Vc / E = -26 dB

La différence entre les deux est de : -26–(-20)=-26+20=-6 dB

- 20 dB par décade

Exemple : prenons la décade 10 Khz – 100 Khz du tableau précédent :

À 10 Khz, Vc / E = -20 dB

À 100 Khz, Vc / E = -40 dB

La différence entre les deux est de : -40–(-20)=-40+20=-20 dB

Filtre passe-bas RL : la réactance de la bobine varie également en fonction de la fréquence. On peut donc aussi concevoir un filtre passe-bas construit avec une bobine et une résistance.

Le circuit d’un tel filtre est le suivant :

XL = 2 π F L

Voyons les différentes valeurs que prend la réactance d’une bobine de 10 mH en fonction de la fréquence du signal qui lui est appliqué (voir tableau ci-après).

Avec une tension d’entrée de 20 volts et une résistance de 1 KΩ en série avec le condensateur, les tensions aux bornes de la résistance R sont les suivantes :

Supposons qu’on applique cette tension VR à une résistance pure de 1000 Ω et calculons les puissances dissipées dans celle-ci à la fréquence de 1 Hz puis à la fréquence de résonance 15.92 Khz : 

À 1 Hz V1 = VR = 20 volts

À 15.92 Khz, V2 = 0.707 x VR = 14.14 volts

P1 = V1²/R = 20²/1000 = 400 mW

P2 = V2²/R = 14.14²/10000 = 200 mW

P2 / P1 = 200 mW / 400 mW = 0.5 soit 50 %

Le signal a perdu 50% de sa puissance. La fréquence de coupure de ce filtre est bien de 15.92Khz.

On remarque que ce filtre comme le filtre précédent coupe les fréquences hautes et laisse passer les fréquences basses. La coupure se produit lorsque R = XL

R = XL   =>  R = 2πFL   =>  FC = R / 2πL = 1000 / 2π x 10 x 10^-3 = 15.92 Khz

b) Filtre passe-haut

Avec une tension d’entrée de 20 volts et une résistance de 10 Ω en série avec le condensateur, les tensions aux bornes de la résistance R sont les suivantes :

On remarque que ce filtre coupe les fréquences basses et laisse passer les fréquences hautes. La fréquence de coupure est ici de 994.7 Hz.

XL = 2 π F L

Avec une tension d’entrée de 20 volts et une résistance de 1 KΩ en série avec le condensateur, les tensions aux bornes de la bobine L sont les suivantes :

Comme le filtre RC précédent, ce filtre coupe les fréquences basses et laisse passer les fréquences hautes. La fréquence de coupure est ici de 15.92 Khz.

c) Filtre passe-bande

Dans plusieurs circuits électroniques_, il est parfois nécessaire de ne laisser passer que certains signaux à des fréquences bien précises et d’en éliminer les autres. Une des applications du circuit « RLC série » à la résonance est un filtre passe-bande.

Étant donné que le courant est partout le même dans un circuit série et que les réactances sont égales à la résonance (XL = XC), les tensions aux bornes des composants L et C sont égales et s'annulent. Par conséquent la tension appliquée au circuit est égale à la tension aux bornes de la résistance.

Comme le courant est maximal à la résonance, la tension aux bornes de la résistance sera aussi maximale comme le montre la figure ci-dessus.

Si on s’arrange pour que XL soit plus grand que R, ce qui est facile en prenant du fil assez gros, le rapport (XL/R) qui est le coefficient de qualité peut être égal à 10, 50, 100, 200, 400 et même plus. Avec un grand coefficient de qualité, la tension descend abruptement de part et d’autre de la fréquence de résonance.

Ce circuit peut être utilisé comme un filtre passe-bande, dans lequel la bande passante est limitée par les fréquences où la tension tombe à 70,7 % de sa valeur maximale.

d) Filtre coupe bande ou éliminateur de bande (Band Stop ou Notch filter)

Une des applications du circuit résonant parallèle (la résonance est obtenue lorsque XL = XC) est le filtre éliminateur de bande montré à la figure suivante :

La fonction de ce type de filtre est d'éliminer les signaux à la fréquence de résonance. En effet, à cette fréquence, l'impédance équivalente du circuit composé de L et C est à son maximum, de sorte que le maximum de tension se retrouve aux bornes de l’ensemble « L et C ». La tension aux bornes de R est alors minimale. Lorsque la fréquence du circuit s'éloigne de sa valeur de résonance, l'impédance équivalente du circuit composé de L et C diminue, ce qui a pour effet d’augmenter la tension aux bornes de la résistance. La largeur de bande ou "Wide Band" (LB ou WB) de ce filtre éliminateur de bande est limitée par les fréquences où la tension tombe à 70,7 % de sa valeur maximale.

1.3. Les filtres actifs

(a) Aux basses fréquences, les bobines sont volumineuses et coûteuses. De plus L varie en fonction de la fréquence en raison des pertes dans le fer. On construit, à l’aide d’amplificateurs opérationnels des filtres actifs à caractéristique décroissante abrupte semblable à celle des filtres LC passifs. Il existe un grand nombre de filtres actifs différents (Butterworth, Chebyshev, Bessel). Le plus répandu est le filtre de Butterworth.

Ce circuit est composé d’un filtre passe bas RC suivi d’un amplificateur opérationnel dont le gain en boucle fermée (CL= Close Loop) est :

Rf

ACL = --------- + 1

       Ri

Ce filtre laisse passer toutes les fréquences jusqu’à la fréquence de coupure FC ; au-dessus de cette fréquence, la caractéristique de réponse en fréquence descend de 20 dB par décade. On appelle un tel filtre "filtre passe bas" ou LPF.

(b) Pôles ou ordres : on utilise souvent le mot "Pôle" ou "Ordre" dans l’étude des filtres. On parle d’un filtre passe bas à un pôle, deux pôles, trois pôles etc.

Pour obtenir le nombre de pôles, on compte le nombre de réseaux de retard. Le circuit précédent est un filtre à un pôle.

(c) Filtre passe bas à deux pôles

Ce filtre comporte deux réseaux de retard. Le calcul mathématique montre que pour le gain en boucle fermée ACL= 1.586, on obtient la caractéristique de réponse la plus horizontale dans la bande médiane de fréquence.

Rf

ACL = --------- + 1 = 1.586   =>  Rf = 0.586 x Ri

      Ri

Si Ri = 1KΩ alors Rf = 0.586 x 1K = 586 Ω (560 Ω normalisée)

Si le gain est inférieur à 1.586, la caractéristique du filtre tend vers un déphasage linéaire en fonction de la fréquence (filtre de Bessel); pour un gain supérieur à 1.586, on obtient des ondulations dans la bande médiane (caractéristique de réponse de Chebyshev).

À la fréquence de coupure, le gain total en tension a diminué de 3 dB. Au-dessus de la fréquence de coupure, le gain en tension diminue de 40 dB par décade (ce qui équivaut à –12 dB par octave).

Le terme – 40 dB / décade signifie que le gain en tension diminue de 100 fois sa valeur lorsque la fréquence augmente de 10 fois sa valeur.

20 log (VOUT/VIN) = -40   =>  log (VOUT/VIN) = -2   =>  (VOUT/VIN) = shift log (-2) = 0.01 ou VOUT = VIN / 100

Ceci équivaut à –12 dB par octave qui signifie que le gain en tension diminue de 4 fois lorsque la fréquence double sa valeur.

20 log (VOUT/VIN) = -12   =>  log (VOUT/VIN) = -0.6   =>  (VOUT/VIN) = shift log (-0.6) = 0.25 ou VOUT = VIN / 4

(d) Filtre passe haut actif à un pôle

La courbe de réponse de ce filtre est la suivante :

(e) Filtre passe haut actif à deux pôles

Ce filtre possède une atténuation de 40 dB par décade au-dessous de FC.

(f) Filtre passe-bande (combinaison d’un filtre passe-haut et d’un filtre passe-bas).

La courbe de réponse de ce filtre est la suivante :

Ce filtre possède une atténuation de 40 dB par décade au-dessous de FC1 et au-dessus de FC2.

(g) Avantage des filtres actifs :

• Permettent des isolations beaucoup plus élevées grâce à leurs impédances d’entrée élevées.

• Peuvent être réalisés sans bobine. Ceci diminue grandement le coût, le poids, la dimension, les effets inductifs (élimine la nécessité d’avoir des blindages magnétiques).

• Permettent d’amplifier le signal en plus de le filtrer.

• Peuvent avoir des fréquences centrales ajustables.

• Leur réponse peut se rapprocher de la réponse idéale.

(h) inconvénients :

• Nécessitent une alimentation.

• Les amplitudes des signaux à filtrer sont limitées par la tension d’alimentation.

1.4. Les niveaux de référence

Le décibel n'est pas une valeur absolue ; c'est un moyen pour préciser le ratio d'un niveau par rapport à un certain niveau de référence. Habituellement quand le niveau de référence est donné, c'est sous cette forme : 775mV dans une impédance de 600 ohms par exemple. Cependant le niveau de référence n'est pas spécifié mais sous-entendu lorsque la valeur du niveau est exprimée en décibels.

Les niveaux de référence les plus utilisés sont les suivants :

dBj   => Référence=1mV

dBmV   =>  Référence=1mV

dBµV  =>  Référence=1µV

dBk   =>  Référence=1KW

dBm   =>  Référence=1mW dans une impédance de 600 Ω (775mV)

ou 1mW dans une impédance de 50 Ω (224mV)

dBs   =>  Référence=Désignation Japonaise pour le système dBm

dBu   =>  Référence Européenne pour le système dBm

dBv   =>  Référence=1V

dBw   =>  Référence=1W

dBrap   =>  Référence=10^-16W (utilisée comme une référence acoustique)

dB   =>  Référence=10^-12W (acoustique)

2. Les oscillateurs

2.1. Introduction

Partout où vous regarder dans le domaine de l'électronique, vous trouverez des oscillateurs. Il y en a dans votre montre, votre téléviseur, vos radios, votre voiture, votre ordinateur. Ils font tous appel au même principe et bien que conçus pour des applications très différentes, répondent aux mêmes critères.

À partir de seulement une alimentation DC à l’entrée du circuit, on obtient une onde alternative répétitive à la sortie. Un oscillateur est donc un circuit qui convertit l’énergie électrique DC en énergie électrique AC.

2.2. Classification

Il existe une grande variété d'oscillateurs comme le montre le tableau ci-dessous.

Sinusoïdaux ou harmoniques	Fixes : RC, LC et quartz Variables : LC, VCO (diodes varicaps)
Non sinusoïdaux ou de relaxation	À relaxation : multivibrateurs trapézoïdaux, rampes, dents de scie

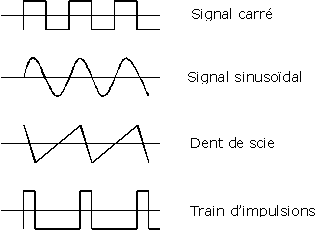
2.3. Oscillateur non sinusoïdal ou de relaxation

Un multivibrateur astable est une horloge qui rythme le fonctionnement des circuits numériques. Son principe est basé sur la charge et la décharge du condensateur C.

2.3.1  Multivibrateur astable à minuterie NE555

Le 555 est un circuit électronique miniaturisé qui est utilisé comme temporisateur. Il est basé sur la stabilité des circuits “RC” pour lesquels on peut prévoir le temps dont ils ont besoin pour atteindre une tension donnée. Les étapes qui suivent vont vous faire découvrir les fonctions des broches de ce circuit intégré très courant.

L'alimentation positive est assurée par la broche 8 ; la tension négative de la source doit être branchée à la broche 1. Les broches sont numérotées selon le schéma ci-dessous ; il y a au moins un marqueur dessiné sur le circuit intégré, soit un point creusé dans le plastique dans un coin du C.I., soit une encoche au centre du C.I. ; la broche 1 se trouve alors immédiatement à gauche de cette encoche ou de ce point selon le cas. Les autres broches sont numérotées dans le sens anti-horaire.

2.3.2. Schéma fonctionnel du 555

La figure ci-dessous représente un schéma fonctionnel d'une minuterie 555, une minuterie intégrée à 8 broches. Le comparateur du haut a une entrée de seuil (broche 6) et une entrée de commande (broche 5). Si l'entrée de commande n'est pas utilisée alors la tension de commande est égale à 2 x (VCC / 3) et lorsque la tension de seuil dépasse la tension de commande, la sortie du comparateur du haut met la bascule au niveau haut.

Le comparateur du bas a son entrée inverseuse, appelée entrée de basculement, reliée à la broche 2. L'entrée non inverseuse a une tension fixe de VCC / 3. Lorsque la tension d'entrée de basculement est légèrement inférieure à VCC / 3, la sortie de l'amplificateur opérationnel passe au niveau haut et remet la bascule au niveau bas.

Le collecteur du transistor à décharge est relié à la broche 7. Lorsque cette broche est raccordée à un condensateur externe de minutage, la sortie Q de niveau de la bascule sature le transistor et décharge le condensateur. Lorsque Q est au niveau bas, le transistor s'ouvre et le condensateur se charge. Le signal complémentaire de la bascule passe à la broche 3.

Et enfin si la sortie externe de remise à niveau bas (broche 4) est mise à la masse, le dispositif est inhibé (ne peut fonctionner).

2.3.3. Fonctionnement en Oscillateur

Comme le condensateur ne se charge ni ne se décharge complètement, la fréquence d'oscillation est d'environ F = 1 / 2.2 x R1 x C1

Dans le cas de ce montage C se charge à travers de deux résistances en série (20K) et se décharge à travers une résistance de 10K par l’intermédiaire du transistor interne du 555. Les temps hauts et les temps bas du signal sont dans un rapport de 2. La sortie est donc un signal rectangulaire et non carré comme dans le circuit précédent.

W = largeur de l’impulsion, D = coefficient d’utilisation ou Duty cycle

Rappel 1 : la charge d’un condensateur suit une loi exponentielle. La tension aux bornes d’un condensateur à un moment donné durant sa charge est donnée par la relation suivante :

E = (E final – E initial) (1 – e^{– W/RC})

Exemple: La tension d’alimentation est de 15 volts et on veut connaître la valeur de la tension après 1τ et après 5τ, le condensateur étant initialement déchargé 

1τ = RC  =>  W = RC   =>  W/RC = RC/RC = 1

donc E = (15 – 0) (1 – e^-1) = 15 – 15 x e^-1 = 15 – 15 x 0.3679 =15 – 5.52 = 9.48 volts soit en % : 9.48 x 100 /15 = 63.2 %

5τ = 5RC   =>  W = 5RC   =>  W/RC = 5RC/RC = 5

donc E = (15 – 0) (1 – e^-5) = 15 – 15 x e^-5 = 15 – 15 x 0.0067 =15 – 0.1 = 14.9 volts soit en % : 14.9 x 100 /15 = 99.3 %

Rappel 2 : On charge un condensateur aux 2/3 de la valeur de la tension d’alimentation et on veut connaître le temps que durera cette charge soit W.

La relation précédente s’écrit :

(2/3) Vcc = Vcc (1 – e^{- W/RC}) = Vcc – Vcc x e^{- W/RC}   =>  e^{- W/RC} = 1/3

=> W = -RC x ln (1/3) = -RC x (-1.1) = 1.1x RC

Si le coefficient d’utilisation est de 50 %, la fréquence est alors définie par la relation suivante:

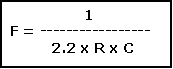
Rappel 3 : Dans le cas de l’oscillateur à minuterie 555, la charge du condensateur commence à VCC / 3 et se termine à 2 x VCC / 3 avec une tension cible (tension d’alimentation) de Vcc.

2 x Vcc      Vcc                   Vcc

-------- = -------- + ( Vcc - -------)(1 – e^{- W/RC})

   3             3                      3

  Vcc          2 x Vcc     2 x Vcc

-------- = ( ---------) – ---------- e^{- W/RC})

   3               3             3

    Vcc          2 x Vcc

- -------- = – ---------- e^{- W/RC})

     3                                           3     

e^{- W/RC}= 0.5   =>  W/RC = - ln 0.5 = 0.693

Temps de charge : W = 0.693 (R1 + R2) x C1

Temps de décharge T – W = 0.693 x R2

Période : T = 0.693 (R1 + R2) x C1 + 0.693 R2 x C1

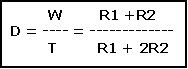
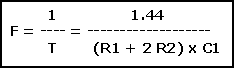
2.3.4. Oscillateur à fréquence réglée par variation de tension

La figure ci-dessus représente un oscillateur à fréquence réglée par variation de tension, une application d’une minuterie 555. On appelle parfois ce dispositif un convertisseur tension-fréquence parce que la tension d’entrée fait varier la fréquence de sortie.

La broche 5 (commande) est raccordée à l’entrée inverseuse du comparateur du haut. Normalement la tension de commande est égale à 2Vcc/3 en raison du diviseur interne de tension. La tension provenant de l’extérieur (potentiomètre) a préséance sur la tension interne, autrement dit, on fait varier la tension de commande en ajustant le potentiomètre. Les temps de charge et de décharge varient en fonction de cette tension de commande et par conséquent la fréquence de sortie varie aussi.

Lorsque la tension de commande augmente, la fréquence diminue et vice versa.

2.4. Oscillateur simple

Un oscillateur est un montage capable d’engendrer des vibrations périodiques en fonction du temps. Un pendule, par exemple, est un oscillateur mécanique. Lorsqu’on le déplace de sa position d’équilibre, il décrit un mouvement, de va et vient, répété. Un pendule oscillant que l’on abandonne à lui-même effectue un certain nombre d’oscillations d’amplitude décroissante puis s’arrête. À ce moment, toute l’énergie mécanique de départ a été absorbée par les frottements.

Si l’on veut entretenir le mouvement à amplitude constante, il faut apporter à chaque cycle une quantité d’énergie juste égale à celle qui a été absorbée. C’est ce que l’on fait dans les horloges à balancier par l’intermédiaire d’un ressort tendu.

Une cloche, une corde de guitare ou de violon sont des oscillateurs mécaniques qui ont la propriété d’émettre des sons audibles à l’oreille humaine. L’atome lui-même constitue un oscillateur miniature dans lequel les électrons sont en "résonance" autour du noyau. Le LASER est tout simplement un oscillateur lumineux.

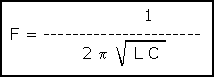
Le plus simple des oscillateurs électroniques est le circuit résonant pur formé d’une inductance pure et d’un condensateur pur (sans résistance). Lorsque la capacité initialement chargée est reliée à l’inductance, l’énergie électrique se met à osciller entre la self et la capacité avec une fréquence égale à :

Dans un circuit LC réel, nous retrouvons une situation semblable à celle du pendule. Les oscillations sont amorties, cette fois à cause de la résistance électrique du circuit. L’énergie électrique initialement emmagasinée dans le condensateur est dissipée cycle après cycle, sous forme de chaleur. Pour maintenir l’amplitude des oscillations constante, il faudrait communiquer au circuit LC des impulsions suffisamment énergiques pour compenser les pertes par effet Joule (chaleur).

La figure suivante donne un montage possible avec transistor. Les impulsions que reçoit la base sont amplifiées et transmises au circuit LC qui oscille au rythme des impulsions d’entrée.

Cette solution n’est pas satisfaisante puisque pour faire fonctionner un oscillateur, on a besoin d’un autre oscillateur.

2.5. Oscillateur à réaction

Au lieu de faire appel à un oscillateur auxiliaire, on prélève une fraction du signal amplifié et on le retourne dans le circuit d’entrée. Cette opération est appelée réaction positive ou rétroaction

Un oscillateur est composé d'un amplificateur duquel on prélève une partie du signal de sortie que l'on réinjecte vers l'entrée.

Nous avons déjà fait cela mais dans le but de stabiliser l'amplificateur, d'augmenter sa bande passante et surtout de ne pas le transformer en oscillateur.

Dans le cas de l’oscillateur, le signal prélevé de la sortie sera réinjecté en phase. C’est ce qu’on appelle la réaction positive.

La réaction positive consiste à prélever une fraction du signal amplifié et de la retourner dans le circuit d’entrée avec un déphasage de 0 degré.

Le report d’énergie est effectué par un circuit RC, LC ou un cristal (quartz). Si le sens des connexions est convenable, le courant de base tend à renforcer le courant de collecteur qui lui a donné naissance et le système tombe en régime d’auto entretien. Ce phénomène est appelé oscillation.

Si nous appelons A le gain et l'amplificateur et b le gain du système de réaction, le critère de BARKHAUSEN définit la condition pour que le système entre en oscillation.

Considérons séparément chacun des deux éléments constitutifs d’un oscillateur

Nous supposerons que l’amplificateur fonctionne en régime linéaire : à tout signal sinusoïdal appliqué à son entrée, correspond un autre signal, lui aussi sinusoïdal, recueilli sur sa sortie. Si V1 et V2 sont les amplitudes respectives de ces tensions, on appelle gain de l’amplificateur, le rapport :

        V2

A = -------

        V1

Généralement, l’amplificateur introduit non seulement un gain, mais aussi un déphasage entre les deux sinusoïdes, que nous noterons f1.

Ces mêmes notions s’appliquent au réseau de rétroaction, bien que ce réseau soit passif. Quelle soit la structure de ce réseau, on peut définir son gain, rapport des amplitudes V4 et V3.

          V4

b = ----------

          V3

Généralement, le réseau de rétroaction atténue le signal qu’on lui applique, de sorte que b est inférieur à l’unité. Pour sa part, ce réseau introduit un déphasage que nous noterons f2.

Relions maintenant les deux éléments en série (voir figure ci-dessus). La sortie de l’amplificateur attaquant l’entrée du réseau passif, nous aurons à la fois

V4 = A x b x V1

f = f1 + f2

(A x b) est appelé gain en boucle ouverte

f est le déphasage total

Si V4 est supérieur à V1 et que le déphasage total est soit nul soit égal à un multiple de 360^o, on obtient l’auto entretien des oscillations en refermons le montage sur lui-même.

A x b ≥ 1

f1 + f2 = 0^o ± 360^o x K

En boucle fermée, le produit b x VOUT s’additionne à VIN, de sorte que :

VOUT = A VIN + A b VOUT   =>  VOUT – A b VOUT = A VIN   => VOUT (1 – A b) = A x VIN

D’où :

VOUT           A

------ = -----------

VIN         1 – A b

Pour différentier ce gain du gain en boucle ouverte, on le notera ACL (CL est mis pour close loop).

          VOUT         A

ACL = ------ = ------------

          VIN        1 – A b

Une fois amorcée, l'oscillation se maintient pour A x b = 1

Si A x b < 1 l'oscillation cesse.

Si A x b > 1, l’amplitude des oscillations augmente jusqu’à la saturation de l’amplificateur. Le signal de sortie ressemblera plus à un signal carré qu’à une sinusoïde.

Dans le cas d’un amplificateur émetteur commun, c’est la contre réaction introduite par la résistance d’émetteur RE qui joue le rôle de limiteur de sorte que l’amplificateur ne sature jamais.

Le réseau de rétroaction ou de réaction positive devra prendre en compte le montage utilisé, déphaser ou pas le signal et appliquer le taux qui convient à l'entrée.

Comment réinjecter la sortie vers l'entrée ?

Il existe plusieurs méthodes, celles-ci sont d'ailleurs constitutives et descriptives du montage. Tel que les classiques : Colpitts, Pierce, Hartley (du nom des inventeurs), voyons quels sont les procédés de couplages les plus fréquemment utilisés.

En fonction du type de montage utilisé, (souvenez-vous, il y a trois montages fondamentaux pour le transistor) nous appliquerons ou pas un déphasage au signal prélevé.

Émetteur commun : déphase de 180°

Collecteur commun : ne déphasage pas

Base commune : ne déphasage pas

Un dernier point à vérifier : l’oscillateur démarre-t-il tout seul dès la mise sous tension ? Oui. En effet, pour que les oscillations prennent naissance dans un circuit LC, il faut que son état de repos soit perturbé. Or, le simple fait de fermer l’interrupteur qui alimente l’oscillateur provoque une “secousse” électrique capable de déclencher l’état oscillatoire. Il y a aussi les dérives thermiques, les tensions de bruit, qui pourraient jouer le même rôle.

2.6. Le réseau RC ou oscillateur à déphasage :

l'amplificateur est un amplificateur émetteur commun, c-à-d que le signal de sortie est déphasé de 180° par rapport à l'entrée.

Cet amplificateur est polarisé en classe A de manière à offrir un signal le plus pur possible. Nous verrons dans cette section que ce n'est pas une exigence systématique.

Le réseau de déphasage et d'injection comporte 3 cellules RC identiques, d'une part pour déphaser le signal de 180° (60° par cellule) et d'autre part pour atténuer le signal à injecter vers l'entrée car nous n'avons pas besoin d'injecter un signal énorme si nous tenons à conserver en sortie un signal sans distorsion.

Ce type d'oscillateur est sélectif, la fréquence d'oscillation est dictée par les valeurs du réseau RC.

Remarque : certaines alimentations nécessitent un condensateur de découplage C5. Ce condensateur met la borne supérieure de la source d’alimentation à la masse en alternatif pour empêcher son impédance de modifier la fréquence d’oscillation et l’amplitude du signal généré.

2.7. Oscillateur à pont de Wien

L’oscillateur à pont de Wien est très couramment utilisé pour réaliser des oscillateurs dont la fréquence peut varier de 1 Hz à 1 Mhz. Les raisons de ce succès sont les suivantes :

a)    La valeur de la fréquence dépend d’une résistance et d’une capacité, composants qu’il est plus facile d’obtenir que les bobines avec un haut degré de qualité;

b)      Le circuit est très stable et le signal très peu distordu;

c)       La fréquence peut être réglée de façon continue.

La partie fondamentale d’un oscillateur à pont de Wien est un réseau, passe-bas passe-haut, tel que celui de la figure suivante :

R1 et C1 forment la portion “passe-bas” du circuit, tandis que R2 et C2 forment la portion “passe-haut”.

Le principe de fonctionnement est simple : à des fréquences basses, le circuit “passe-haut” est dominant dû à la réactance élevée de C2. Au fur et à mesure que la fréquence augmente, XC2 diminue permettant à la tension de sortie d’augmenter. À une certaine fréquence spécifiée, le circuit “passe-bas” prend la relève et Xc1 diminue. 

XC1 diminuant avec l’augmentation de la fréquence, la tension de sortie est alors décroissante comme le montre la courbe de réponse suivante :

Cas particulier R1 = R2 et C1 = C2 et sachant qu’à la résonance R = XC, alors VOUT = VIN / 3

    Vin = (Z1 + Z2 ) x I;            Vout = Z2 x I

    Le gain A = Vout / Vin = Z2 x I / [(Z1 + Z2) x I] = Z2/(Z1+Z2) 

La fréquence de résonance quant à elle est Fr = 1 / 2πRC

Le circuit, passe-haut passe-bas, est utilisé dans la boucle de rétroaction positive de l’amplificateur opérationnel et un diviseur de tension est utilisé dans la boucle de rétroaction négative.

La condition de déphasage de 0 degré est établie lorsque la fréquence est égale à Fr puisque le déphasage autour du circuit réseau RC est 0 degré et que l’amplificateur est non-inverseur.

La condition de gain égal à 1 est établie lorsque le gain en boucle fermée de l’AOP est égal à 3 ce qui annule l’atténuation de 1/3 du réseau RC.

Au départ, le gain en boucle fermée de l’AOP doit être supérieur à 3 jusqu’à ce que le signal de sortie se développe jusqu’à un niveau désiré. Le gain doit ensuite diminuer à 3 pour que le signal de sortie reste à ce niveau.

Le circuit de la figure suivante illustre une méthode de base pour obtenir la condition d’oscillation décrite.

R3 sert à ajuster l’amplitude du signal de sortie. Les diodes 1N4148 vont limiter le gain en boucle fermée de l’AOP à 3. Lorsque le signal est assez fort, les diodes conduisent alternativement et mettent R3 en parallèle avec R1, ce qui diminue le gain en boucle fermée de l’AOP.

La diode Led permet de signaler le fonctionnement de l’oscillateur. Et la diode 1N4148 à ses bornes permet de la protéger lors de sa polarisation inverse pour ne pas la détruire (se rappeler que sa tension maximale en inverse est de 3 volts).

 

2.8. Oscillateur LC : le schéma fondamental est le suivant :

Le principe est la rétroaction du signal de sortie vers l'entrée. Il est composé d'une self et d'un condensateur. L'un ou les deux éléments peuvent être variables pour faire varier la fréquence d'oscillation.

La fréquence d'oscillation sera déterminée majoritairement par la valeur de L et de C et accessoirement par les capacités parasites du montage (elles existent toujours).

On évaluera approximativement la fréquence d'oscillation par la classique formule de Thomson tirée du non moins célèbre :

LCw² = 1 (XL = XC)

Le report d’énergie est effectué par couplage électromagnétique entre la bobine L associée au condensateur C et la bobine L2 de réaction. Si le sens des connexions est convenable, le courant de base tend à renforcer le courant de collecteur qui lui a donné naissance et le système tombe en régime d’auto entretien.

Un dernier point à vérifier : l’oscillateur démarre-t-il tout seul dès la mise sous tension ? Oui. En effet, pour que les oscillations prennent naissance dans un circuit LC, il faut que son état de repos soit perturbé. Or, le simple fait de fermer l’interrupteur qui alimente l’oscillateur provoque une "secousse" électrique capable de déclencher l’état oscillatoire. Il y a aussi les dérives thermiques, les tensions de bruit, qui pourraient jouer le même rôle.

Un type d’oscillateur à résonance est le Colpitts, appelé ainsi en l’honneur de son inventeur.

Cet oscillateur utilise un circuit LC dans la boucle de rétroaction pour fournir le déphasage nécessaire et agir comme un filtre pour ne laisser passer que la fréquence spécifiée d’oscillation. La fréquence approximative d’oscillation est établie par les valeurs de C1, C2 et L selon la formule :

CT étant la capacité équivalente de C1 et C2 en série car les deux condensateurs apparaissent en série dans le circuit résonant.

CT = C1 x C2 / (C1 +C2)

Un autre type d’oscillateur à résonance est le Hartley, qui est semblable à l’oscillateur Colpitts à l’exception que le circuit de rétroaction est constitué de deux bobines et d’un condensateur.

Sa fréquence d’oscillation est donnée par :

LT est la combinaison série de L1 et L2

Un oscillateur à cristal est essentiellement un oscillateur à circuit accordé qui utilise un quartz comme circuit résonant. D’autres types de cristaux peuvent être utilisés mais le quartz est le plus couramment utilisé. Il offre une plus grande stabilité de la fréquence.

Le quartz est composé de silice SiO2, qui est une matière minérale extrêmement répandue dans la nature.

Il se présente soit sous la forme de grands cristaux incolores, colorés ou fumés, soit sous la forme de cristaux microscopiques d'aspect translucide.

Le quartz présente la particularité d'être piézo-électrique, en d'autres termes cela signifie que si nous lui appliquons une force de compression sur ses faces, nous constatons l'apparition de charges électriques.

Si maintenant nous inversons l'effort que nous appliquons sur la lamelle de quartz et qu'au lieu de compresser celui-ci nous exercions une traction, nous constatons que le signe des charges s'inverse. Plus l'effort mécanique est important, plus il y a de charges qui apparaissent.

Mais l'effet piézo-électrique ne s'arrête pas là, il est réversible, càd qu'en appliquant une tension électrique sur la lamelle de quartz, on observe une déformation mécanique. Le quartz est un matériau élastique (toutes choses égales par ailleurs) et il retrouve sa forme originelle dès que cesse la tension.

Ceci est important puisque cela dicte la fréquence propre de résonance qui est liée, entres autres, aux dimensions physiques de la lamelle de quartz.

Sur le plan électrique :

Voici le symbole du quartz :

La lamelle de quartz est reliée grâce à deux électrodes de connexion. Observez le dessin, on devine facilement que les connexions notées A et B vont constituer une magnifique capacité et cette capacité sera la capacité de connexion.

Schéma électrique équivalent d'un quartz :

On remarque immédiatement qu'il s'agit d'un circuit série shunté par une capacité, cette capacité est la capacité due aux connexions. Les valeurs de L, R et C1 sont dictées par la nature et les caractéristiques du quartz.

Comportement électrique du quartz :

Appliquons à un quartz une tension alternative sinusoïdale, faisons la varier et mesurons l'impédance du quartz pour chaque fréquence. Nous obtenons ceci :

Attention, la courbe est beaucoup plus arrondie que cela, seule l'allure générale est  restituée par ce dessin. Hormis ceci, il n'y a pas de réelle surprise pour nous, nous reconnaissons typiquement la réaction d'un circuit série. Quand on approche de la résonance, notée Fs, l'impédance passe par un minimum équivalant sensiblement à R, puis remonte rapidement vers un maximum à la fréquence notée Fp simulant ainsi un circuit parallèle.

Donc tout se passe comme si nous étions en présence d'un circuit série pour une fréquence donnée et d'un circuit parallèle pour une fréquence légèrement supérieure. Ces deux fréquences Fs et Fp sont les fréquences de résonance du quartz.

Comme tout circuit, le quartz a un coefficient de qualité, noté "Q" mais son "Q" est très élevé. On se souvient qu'un Q élevé est gage d'une grande sélectivité et de forts coefficients de surtension, on le calcule par Lw/R. L'ordre de grandeur est compris entre 10⁴ et 10⁶.

La taille mécanique du quartz influe fortement sur ses caractéristiques électriques.

Un quartz dissipe de la puissance, et il convient de ne pas dépasser le maximum tolérable dans un montage oscillateur sous peine de dommages irréversibles.

Son utilité dans les oscillateurs :

Du fait de son Q très élevé et de sa stabilité, le quartz va permettre de contrôler très précisément la fréquence d'oscillation. Dès que l'on aura besoin d'une fréquence stable, on aura recours au quartz.

Exemples d’oscillateurs à cristal :

La figure suivante montre un oscillateur Colpitts modifié qui utilise un cristal en mode de résonance parallèle.

La figure ci-dessous montre quant à elle un oscillateur utilisant un cristal comme un circuit résonant série. L’impédance du cristal est minimale lors de la résonance série, ce qui fournit une rétroaction maximale.

Le condensateur CC sert d’accord pour le cristal afin d’ajuster la fréquence avec précision.

Plage de verrouillage :

Elle définit l’étendue de la fréquence au voisinage de Fo dans laquelle le PLL peut maintenir le verrouillage avec le signal d’entrée. Cette plage est aussi appelée plage de maintien et elle augmente en même temps que le gain de boucle.

Gamme de capture :

Cette gamme définit l’étendue de fréquences au voisinage de Fo pour lesquelles le système peut établir ou acquérir le verrouillage avec le signal d’entrée. Elle est aussi appelée plage d’acquisition, elle est toujours plus petite que la gamme de verrouillage et est en étroite relation avec la bande passante du filtre de boucle. Elle décroît en même temps que la bande passante du filtre diminue.

La plage de verrouillage et de capture peut être illustrée par les courbes de la figure ci-après :

Pour la courbe "aller" la fréquence augmente progressivement, la courbe ne répond au signal d’entrée que lorsque la fréquence est supérieure à la limite inférieure F1 correspondant à la limite inférieure de la plage de capture. La boucle se verrouille alors sur le signal d’entrée en créant une tension d’erreur négative. Puis la tension d’erreur varie avec la fréquence qui passe par Fo. La poursuite fonctionne jusqu’à ce que la fréquence atteigne F2 correspondant à la limite maximale de la plage de verrouillage. Le PLL est hors verrouillage et la tension d’erreur s’annule.

Pour la courbe "retour" la fréquence d’entrée diminue au même rythme que précédemment, le cycle est modifié et devient le suivant : la boucle est asservie à partir de F3 et la poursuite fonctionne jusqu’à F4.

Les bandes délimitées par F1 et F3 et F2 et F4 correspondent aux plages de capture et de verrouillage du système.

Le PLL est donc composé d’un comparateur de phase, d’un filtre passe bas (LPF) et d’un oscillateur dont la fréquence est commandée ou asservie par une tension DC (VCO = Voltage Controlled Oscillator). On dit aussi que c’est un convertisseur tension-fréquence.

En radio et en télévision, la sortie verrouillée est appliquée au mélangeur (Mix) pour utilisation (production de la fréquence intermédiaire).

IF = Fo - Fc (Fo = fréquence de l’oscillateur local, Fc = fréquence de la station syntonisée).

IF1 = 10.7 Mhz, IF2 = 455 Khz en radio AM et 10.7 Mhz en radio FM, 41.25 Mhz pour le son en télévision, 45.75 Mhz pour l’image en télévision.

b) La commande par synthèse de fréquence et microprocesseur

Lorsque le système PLL est programmable c’est à dire que sa fréquence de sortie est variable en fonction de la demande, on l’appellera "synthétiseur de fréquence".

Principe de la synthèse de fréquence

Le principe consiste à contrôler la fréquence de l'oscillateur local des sélecteurs de syntonisation. Afin d'obtenir une grande stabilité de l'oscillateur local, on le compare à un oscillateur à quartz par l'intermédiaire d'un diviseur programmable.

En changeant le rapport diviseur, on modifie la fréquence de l'oscillateur donc la fréquence de l'accord RF du récepteur.

Le taux de division correspondant à chaque canal est contenu dans une mémoire morte R.O.M. du microprocesseur. Le transfert d'un taux de division appelé par l'utilisateur vers le diviseur programmable permet le réglage de l'appareil sur la station désirée.

Pour opérer la sélection des canaux, il suffit donc de modifier le rapport de division N conformément au canal désiré.

Exemple de la synthèse de fréquence en radio mobile CNR-136 (40 canaux)

26.965 Mhz à 27.405 Mhz, IF1 = 10.7 Mhz

Fréquence de l'oscillateur local = Fréquence reçue - I F = 16.27 Mhz Mhz à 16.71 Mhz

Les nombres N = 1627 à 1671 correspondent aux 40 canaux autorisés. 1627 correspond au canal 1, 1671 au canal 40, 1628 au canal 2 etc. (voir tableau correspondant ci-dessous).

1^e canal: 16.27 Mhz / 1627 = 10000 Hz

2^e canal: (16.27 Mhz + 10 Khz) / 1628 = 10000 Hz

3^e canal: (16.27 Mhz + 10 Khz + 10 Khz) / 1629 = 10000 Hz

etc.

Exemple de comparateur de phase : Le OU exclusif

Le signal alternatif de sortie est converti en une tension continue, par un filtre actif passe-bas, qui sera appliquée au VCO.

Le VCO (Voltage Controlled Oscillator) contrôle les variations de cette tension en provenance du filtre et les convertit en variation de fréquence.

c) Caractéristiques du tuner à PLL