
Chap. 2 : Fonctions logiques de base et leurs tables de vérité
Chap. 3 : Les opérateurs mixtes
Chap. 5 : Simplification des circuits logiques
Chap. 8 : Compteurs asynchrones
Chap. 9 : Décompteur asynchrone
Chap. 10 : Afficheur 7 segment et décodeur DCB
Analogique,
Numérique
Système
décimal
Système
binaire
Système
octal
Système
hexadécimal
Conversion
de systèmes
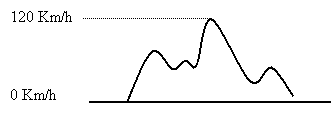
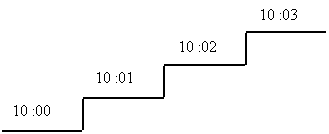
Représentation numérique : une grandeur que l’on représente numériquement n’est pas proportionnelle à une autre grandeur. Exemple : horloge numérique : l’heure du jour est une variable continue alors que les chiffres de l’affichage numérique eux ne varient pas continûment. L’heure affichée progresse par pas d’une minute ou d’une seconde selon le cas.
Grandeur numérique = grandeur discontinue ou discrète.
Systèmes de numération : de nombreux systèmes de numération sont utilisés en technologie numérique. Les plus courants sont les systèmes décimal, binaire, octal et hexadécimal.
1. Système décimalLe système décimal comprend 10 nombres ou symboles qui sont :
0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
En utilisant ces symboles comme chiffres dans un nombre, on parvient à exprimer n’importe
quelle grandeur. Le système décimal est aussi appelé système à base 10.
La valeur d’un chiffre dépend de sa position
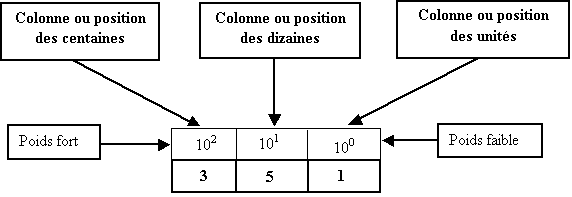
Chaque symbole est multiplié par le poids relatif de sa colonne
351 = 3 x 100 + 5 x 10 + 1 x 1 = 300 + 50 + 1 = 351
Le même principe s’applique pour les nombres décimaux. Après le point décimal, le poids des colonnes est successivement 10-1= 0.1, 10-2= 0.01, 10-3 = 0.001 etc.
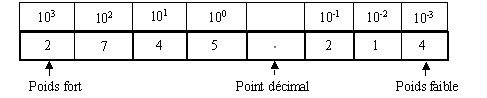
2745.214 = 2 x 1000 + 7 x 100 + 4 x 10 + 5 x 1 + 2 x 0.1 + 1 x 0.01 + 4 x 0.01
Dans le système binaire, il n’y a que deux symboles ou chiffres possibles : 0 et 1.Malgré cela, ce système à base 2 peut représenter n’importe quelle grandeur exprimée dans le système décimal ou dans d’autres systèmes de numération. Chaque chiffre binaire est affecté d’un poids exprimé comme une puissance de 2.
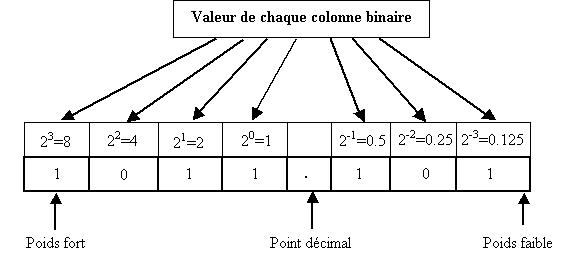
Chaque symbole est multiplié par le poids relatif de sa colonne :
1011.1012 = (1 x 23) + (0 x 22) + (1 x 21) + (1 x 20) + (1 x 2-1) + (0 x 2-2) + (1 x 2-3)
= 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125
= 11.62510
Les indices (2 et 10) indiquent la base dans laquelle le nombre est exprimé.
Dans le système binaire, l’expression chiffre binaire est souvent abrégée en bit (contraction de binary digit).
Comptage binaire : avec 4 bits, on peut compter de 0 à 15 (24 – 1 = 15)
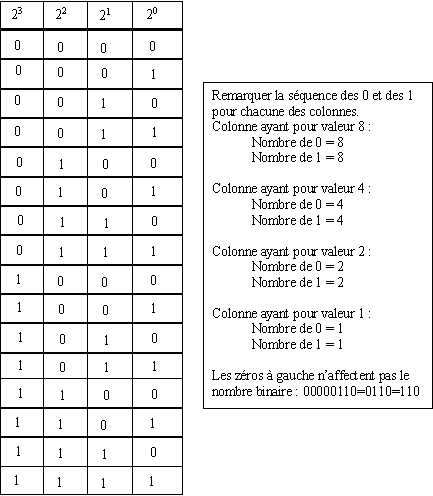
Exercices :
1. Quel est le plus grand nombre que l’on peut représenter au moyen de 8 bits ? Exprimer ce nombre en décimal et en binaire.
28 –1 = 256 – 1 = 25510 = 111111112
2. Donner l’équivalent décimal de 11010112
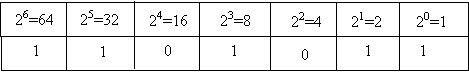
11010112 = 1 x 64 + 1 x 32 + 0 x 16 + 1 x 8 + 0 x 4 + 1 x 2 + 1 x 1 = 64 +32 + 8 + 2 + 1 => 11010112= 10710
3. Indiquer le nombre binaire qui suit 101112 dans la suite des nombres binaires.
101112 + 1 = 110002
4. Quel est le plus grand nombre décimal représentable avec 12 bits ?
212 – 1 = 409510
Ce système a comme base huit, ce qui signifie qu’il comprend huit symboles possibles soit 0, 1, 2, 3, 4, 5, 6 et 7. Voici le poids de chacune des positions d’un nombre octal
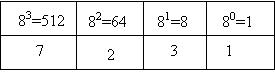
72318 = 7 x 512 + 2 x 64 + 3 x 8 + 1 x 1 = 3584 + 128 + 24 + 1 = 373710
Exercice : Convertir le nombre octal 372 en décimal
3728 = 3 x 64 + 7 x 8 + 2 x 1 = 192 + 56 + 2 = 25010
Le système hexadécimal a comme base 16, ce qui nécessite 16 symboles, qui sont les dix chiffres 0 à 9 plus les lettres majuscules A, B, C, D, E et F. Les lettres A, B, C, D, E et F ont respectivement comme valeur décimale 10, 11, 12, 13, 14 et 15.
|
Hexadécimal |
Décimal |
|
0 |
0 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
8 |
|
9 |
9 |
|
A |
10 |
|
B |
11 |
|
C |
12 |
|
D |
13 |
|
E |
14 |
|
F |
15 |
Voici le poids de chacune des positions d’un nombre hexadécimal
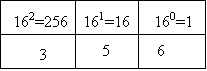
35616 = 3 x 256 + 5 x 16 + 6 x 1 = 768 + 80 + 6 = 85410
Exercice : Convertir le nombre hexadécimal 2AE16 en décimal
2AE16 = 2 x 256 + 10 x 16 + 14 x 1 = 512 + 160 + 14 = 68610
5.1. Conversion binaire-décimal : tout nombre binaire peut être transformé en son équivalent décimal simplement en additionnant les poids des diverses positions où se trouve une valeur « 1 ».
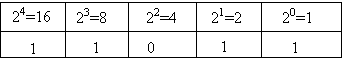
110112 = 1 x 16 + 1 x 8 + 1 x 2 + 1 x 1 = 16 + 8 + 2 + 1 = 2710
Exercice 1 : Convertir le nombre 101101 en son équivalent décimal

1011012 = 1 x 32 + 1 x 8 + 1 x 4 + 1 x 1 = 32 + 8 + 4 + 1 = 4510
Exercice 2 : Convertir le nombre binaire 100011010 en décimal
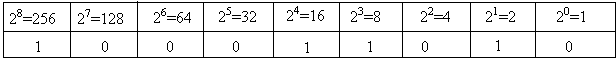
1000110102 = 256 + 16 + 8 + 2 + = 28210
5.2. Conversion décimal-binaire : il existe deux façons de convertir un nombre décimal en son équivalent binaire.
Première méthode : soit à convertir le nombre décimal 45 en binaire

4510 = 32 x 1 + 16 x 0 +8 x 1 + 4 x 1 + 2 x 0 +1 x 1 = 1011012
Exemple 2 : convertir 7810 en binaire
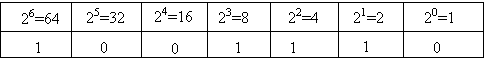
7810 = 64 x 1 + 32 x 0 + 16 x 0 +8 x 1 + 4 x 1 + 2 x 1 +1 x 0 = 10011102
Cette méthode convient aux petits nombres.
2. Deuxième méthode : Répétition de divisions : cette méthode convient mieux aux grands nombres décimaux ; il s’agit de répéter la division par 2 jusqu’à ce que le quotient soit nul.
Exemple : convertir 4510 en binaire
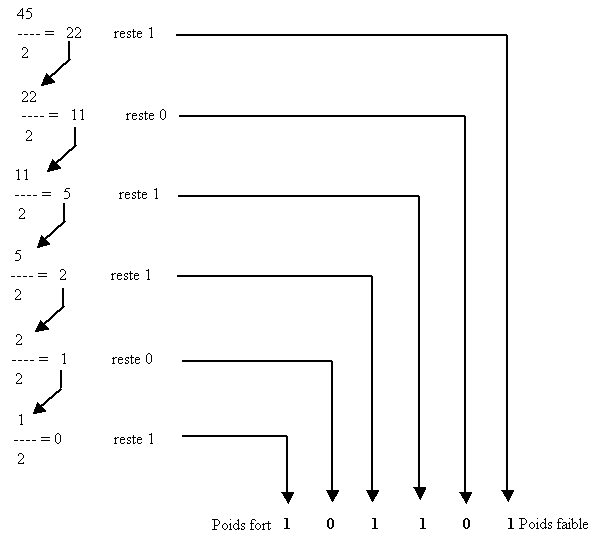
4510 = 1011012
Exercices : convertissez les nombres décimaux suivants en binaire au moyen des deux méthodes exposées : 25, 83 et 729
2510 = 110012
8310 = 10100112
72910 = 10110110012
5.3. Conversion octal-décimal : on convertit un nombre octal en son équivalent décimal en multipliant chaque chiffre octal par son poids positionnel.
Exemple 1 : 3728 = (3 x 82) + ( 7 x 81) + (2 x 80) = 3x 64 + 7 x 8 + 2 x 1 = 25010
Exemple 2 : 248 = 2 x 8 + 4 x 1 = 2010
5.4. Conversion décimal-octal : La méthode est la même que pour la conversion décimal-binaire, mais cette fois-ci en divisant par 8 plutôt que par 2. Voici un exemple :
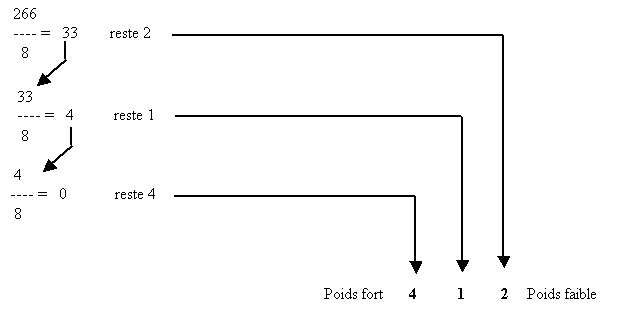
26610 = 4128
5.5. Conversion octal-binaire : le principal avantage du système de numération octal réside dans la facilité avec laquelle il est possible de passer d’un nombre octal à un nombre binaire. Il suffit de transformer chaque chiffre du nombre octal en son équivalent binaire de trois chiffres.
|
Chiffre octal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Équivalent binaire |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Exemple 4128 = 1000010102
5.6. Conversion hexadécimal-décimal : à chaque chiffre hexadécimal est attribué un poids élevé à un e certaine puissance.
Exemple : 11216 => décimal
11216 = (1 x 162) + (1 x 161) + (2 x 160) = 256 + 16 + 2 =27410
5.7. Conversion décimal-hexadécimal : pour convertir un nombre décimal en hexadécimal, il faut procéder de la même façon que la conversion décimal-binaire et décimal-octal, mais cette fois en divisant par 16.
Exemple 1 : convertir 27410 en hexadécimal
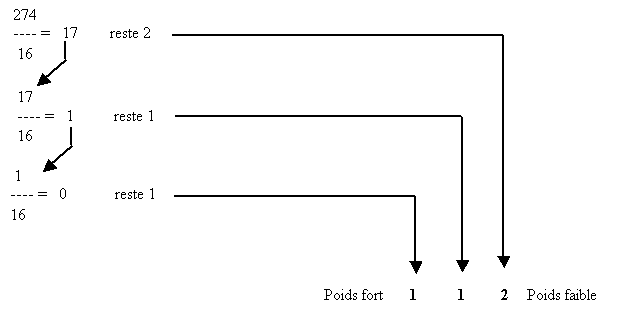
27410 = 11216
Exemple 2 : convertir 21510 en hexadécimal

21510 = D716
5.8 Conversion hexadécimal-binaire : la conversion d’un nombre hexadécimal en un nombre binaire ne pose vraiment pas de difficulté, puisque chaque chiffre hexadécimal est remplacé par son équivalent binaire de 4 bits.
|
Chiffre hexadécimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Équivalent binaire |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
Chiffre hexadécimal |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
Équivalent binaire |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
Exemple : 9F216 = 1001111100102
5.9. Conversion binaire-octal et binaire-hexadécimal : à partir de la gauche, on décompose le nombre binaire en tranches de trois bits pour passer à l’octal et en tranches de 4 bits pour passer à l’hexadécimal puis on attribue à chacun des groupes le chiffre octal ou hexadécimal correspondant.
Exemple : convertir le nombre 1001111100102 en octal et en hexadécimal
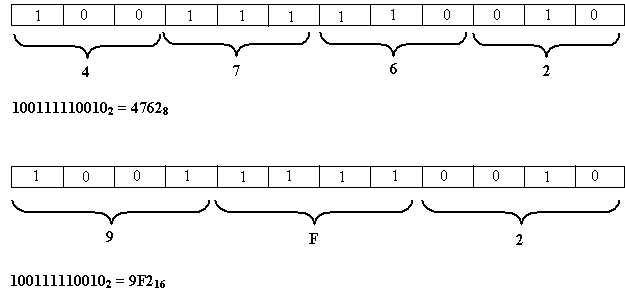
Introduction
Opérateur
OU (OR)
Opérateur
ET (AND)
Opérateur
NON (Inverseur)
Dans le domaine de la logique numérique, on utilise d’autres expressions qui sont synonymes de 0 et de 1.
|
Niveau logique 0 |
Niveau logique1 |
|
Faux |
Vrai |
|
Arrêt |
Marche |
|
Bas |
Haut |
|
Non |
Oui |
|
Ouvert |
Fermé |
Il y a trois fonctions logiques de base :
![]() L’addition logique ou opération OU (OR). Le symbole habituel de
cette opération est le signe +
L’addition logique ou opération OU (OR). Le symbole habituel de
cette opération est le signe +
![]() La multiplication logique ou opération ET (AND). Son symbole
habituel est le signe de la multiplication (.).
La multiplication logique ou opération ET (AND). Son symbole
habituel est le signe de la multiplication (.).
![]() La complémentation ou l’inversion logique, dite aussi opération
NON (INVERTER). Son symbole habituel est une barre de surlignement (-)
La complémentation ou l’inversion logique, dite aussi opération
NON (INVERTER). Son symbole habituel est une barre de surlignement (-)
En électronique numérique une porte « OU » est un circuit ayant au moins deux entrées et dont la sortie est égale à la somme logique des entrées.
Le symbole de la porte « OU » est :
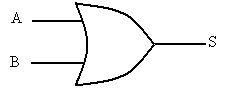
Son équation s’écrit :
S = A + B
Dans cette équation, le signe (+) n’indique pas une addition ordinaire mais plutôt l’addition logique (opération OU) où la sortie du circuit réagit aux diverses combinaisons des niveaux logiques appliqués aux entrées.
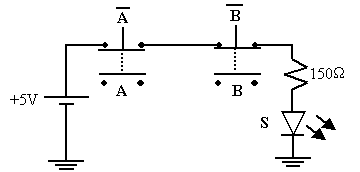
Analysons le fonctionnement à partir du circuit équivalent suivant :
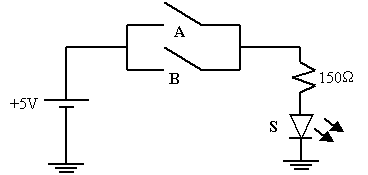
On sait que la LED va s’allumer lorsque la tension à son anode sera positive par rapport à la tension à sa cathode. Ceci se produira si l’on ferme l’interrupteur A, l’interrupteur B ou les deux à la fois. La LED est éteinte si et seulement si les deux interrupteurs sont ouverts.
Ce fonctionnement est illustré par la table suivante que l’on appelle table de vérité :
|
A |
B |
S |
| 0 | 0 | 0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Définition : une porte « OU » a un fonctionnement tel que sa sortie est à un niveau haut (niveau 1) quand au moins une de ses entrées est au niveau haut, à plus forte raison quand les deux entrées sont au niveau haut. Cette porte sera au niveau bas (niveau 0) si toutes ses entrées sont au niveau bas.
Exemple d’une porte « OU » à trois entrées :
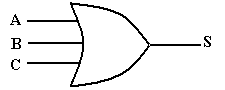
|
A |
B |
C |
S |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Récapitulation de l’opération « OU » : les points importants à retenir sont :
L’opération « OU » donne un 1 si l’une quelconque de ses variables d’entrée est à 1
L’opération « OU » donne un 0 si toutes ses variables d’entrée sont à 0
Dans l’opération « OU » 1+1 =1, 1+1+1=1, etc.
Application : système de régulation industriel (application d’une porte « OU » à un système d’alarme). Le déclenchement de l’alarme se fera si la température ou la pression d’un procédé chimique excède une valeur maximale.
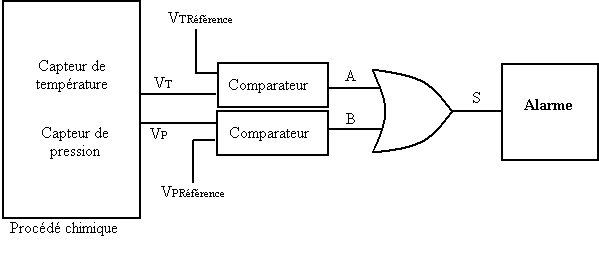
Si deux variables A et B sont combinées par la multiplication logique (opération ET), le résultat S s’exprime symboliquement ainsi :
S = A . B
Dans cette équation, le signe (.) signifie l’opération booléenne « ET »
Comme la porte « OU », la porte « ET » possède au moins 2 entrées, son symbole est :

Analysons son fonctionnement à partir du circuit équivalent suivant :
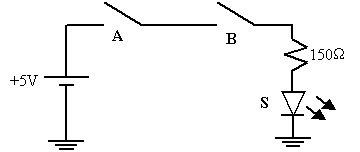
La LED ne s’allumera que si les deux interrupteurs A et B qui sont placés en série sont tous les deux fermés.
La multiplication logique est exactement comme la multiplication ordinaire. Quand A ou B est 0, le produit est nul ; quand A et B sont 1, leur produit est 1.
Dans l’opération « ET » la réponse est 1 si et seulement si toutes les entrées sont à 1 et elle est 0 dans tous les autres cas.
Ce fonctionnement est illustré par la table de vérité suivante :
![]()
|
A |
B |
S |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
L’expression S = A . B qui se lit « S égal A et B » est souvent abrégée S = AB comme en algèbre ordinaire.
Exemple d’une porte « ET » à trois entrées :
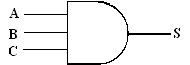
|
A |
B |
C |
S |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Application : déclenchement d’une alarme si une porte est ouverte
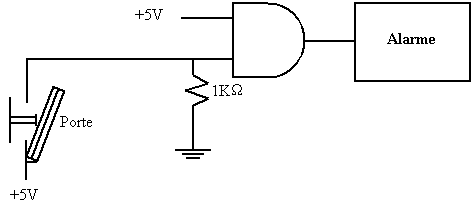
L’opération « NON », contrairement aux opérations « OU » et « ET » ne concerne qu’une seule variable d’entrée. Si une variable A est soumise à une opération « NON », le résultat S est donné par l’expression :
![]()
Le trait de surlignement représente l’opération NON. L’expression se lit :
S égal « NON A »
Ou S égal « Inverse de A »
Ou S égal « Complément de A »
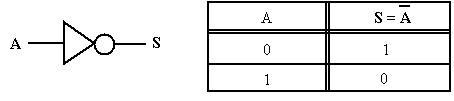
Son symbole est :
![]()
Le circuit suivant explicite son fonctionnement :
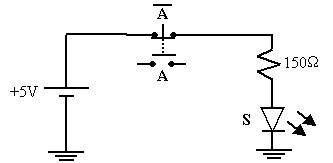
Si A est ouvert, « NON A » qui est un interrupteur normalement fermé est égal à 1, la LED est allumée alors que si A est fermé, « NON A » est égal à 0 et la LED est éteinte.
La table de vérité suivante illustre ce fonctionnement :
Résumé des règles qui régissent les opérations « OU », « ET » et « NON »

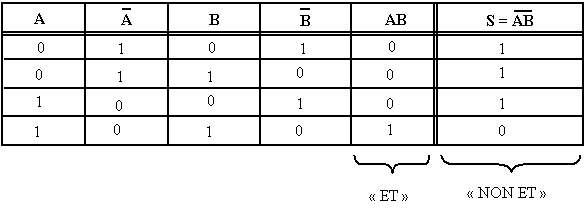
L’opération « NON-ET » est une combinaison d’opérations élémentaires « ET » et « NON »
NON-ET (NAND) = Opérateur « ET » suivi d’un « INVERSEUR ».
L’expression de sortie d’une porte « NON-ET » à deux entrées A, B est :
![]()
Symbole de la porte « NON-ET »
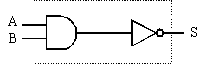
Ce circuit est habituellement représenté par le symbole suivant où le petit rond à la sortie de la porte ET signifie « inversion ».
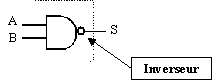
Son fonctionnement peut être compris à partir du circuit suivant :
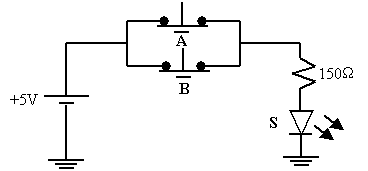
![]()
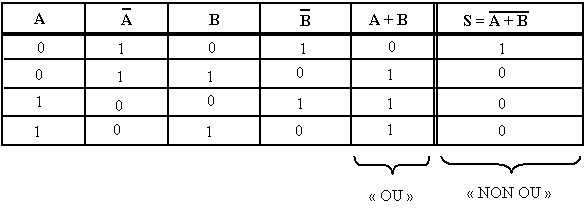
L’opération « NON-OU » est une combinaison des opérations élémentaires « OU » et « NON »
NON-OU (NOR) = Opérateur « OU » suivi d’un « INVERSEUR ».
L’expression de sortie d’une porte « NON-OU » à deux entrées A, B est :
![]()
Symbole de la porte « NON-OU »
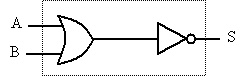
Ce circuit est habituellement représenté par le symbole suivant où le petit rond à la sortie de la porte « OU » signifie « inversion ».
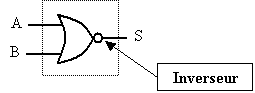
Ce circuit explicite le fonctionnement de cette porte :

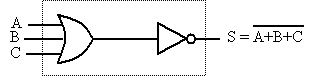
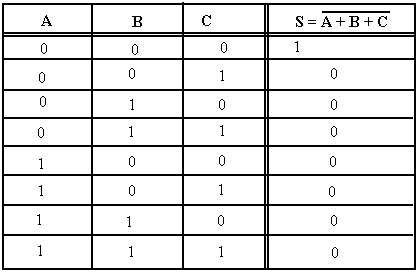
Exercice 1 : Écrire l’expression booléenne pour une porte logique « OU » (ou OR) à trois entrées suivie d’un inverseur.
Exercice 2 : Dessiner le circuit logique correspondant à l’expression :
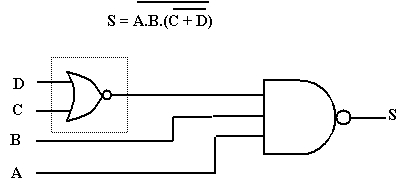
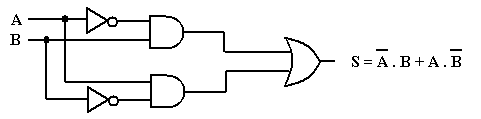
Une porte « OU Exclusif » n’a que deux entrées (il n’existe pas de « OU Exclusif » à 3 ou 4 entrées). Ces deux entrées sont combinées pour donner :
![]()
On abrège cette expression pour l’écrire :
![]()
![]()
La sortie du « OU Exclusif est au niveau haut (1) seulement quand les deux entrées sont à des niveaux différents comme le montrent le schéma équivalent et la table de vérité suivants :
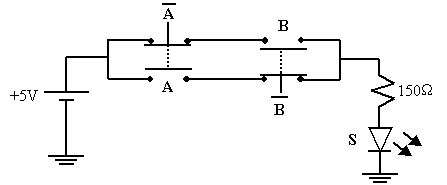

Le symbole du « OU Exclusif » est :
